
آموزش پردازش تصویر _دستور imread
سپتامبر 20, 2020آموزش پردازش تصویر _دستور imwrite
سپتامبر 22, 2020ارزیابی توصیف گرهای رنگ برای تشخیص اشیا و صحنه
|Evaluating Color Descriptors for Object and Scene Recognition
Image category recognition is important to access visual information on the level of objects and scene types. So far, intensity-based descriptors have been widely used for feature extraction at salient points. To increase illumination invariance and discriminative power, color descriptors have been proposed. Because many different descriptors exist, a structured overview is required of color invariant descriptors in the context of image category recognition. Therefore, this paper studies the invariance properties and the distinctiveness of color descriptors (software to compute the color descriptors from this paper is available from http://www.colordescriptors.com) in a structured way. The analytical invariance properties of color descriptors are explored, using a taxonomy based on invariance properties with respect to photometric transformations, and tested experimentally using a data set with known illumination conditions. In addition, the distinctiveness of color descriptors is assessed experimentally using two benchmarks, one from the image domain and one from the video domain. From the theoretical and experimental results, it can be derived that invariance to light intensity changes and light color changes affects category recognition. The results further reveal that, for light intensity shifts, the usefulness of invariance is category-specific. Overall, when choosing a single descriptor and no prior knowledge about the data set and object and scene categories is available, the OpponentSIFT is recommended. Furthermore, a combined set of color descriptors outperforms intensity-based SIFT and improves category recognition by 8 percent on the PASCAL VOC 2007 and by 7 percent on the Mediamill Challenge.
تشخیص دسته تصویر برای دستیابی به اطلاعات بصری در مورد سطح اشیا و انواع صحنه مهم است. تا کنون ، توصیفگرهای مبتنی بر روشنایی به طور گسترده ای برای استخراج ویژگی در نقاط برجسته مورد استفاده قرار گرفته اند. برای افزایش عدم تغییر نسبت به روشنایی و قدرت تمایز بیشتر ، توصیفگرهای رنگی ارائه شده است. از آنجا که توصیفگرهای مختلفی وجود دارد ، از یک توصیف ساختار یافته از توصیف گرهای مقاوم به رنگ در زمینه تشخیص طبقه بندی تصویر لازم است. بنابراین ، این مقاله خصوصیات تغییرناپذیری و متمایز بودن توصیفگرهای رنگ را به صورت ساختاری بررسی می کند (نرم افزاری برای محاسبه توصیفگر رنگ از این مقاله از طریق http://www.colordescriptors.com در دسترس است). خواص تحلیلی توصیف کننده های رنگ ، با استفاده از یک طبقه بندی بر اساس خصوصیات عدم تغییر با توجه به تبدیلات نورسنجی ، بررسی شده و با استفاده از یک مجموعه داده با شرایط روشنایی شناخته شده آزمایش شده است. علاوه بر این ، متمایز بودن توصیفگرهای رنگ با استفاده از دو معیار ، یکی از حوزه تصویر و دیگری از حوزه ویدئو ، به صورت آزمایشی ارزیابی می شود. از نتایج نظری و تجربی می توان نتیجه گرفت که عدم تغییر در تغییرات شدت نور و تغییرات رنگ نور بر شناسایی گروه تأثیر می گذارد. نتایج بیشتر نشان می دهد که ، سودمندی مقاومت نسبت به جابه جایی شدت نور به نوعی خاص است. به طور کلی ، هنگام انتخاب یک توصیفگر منفرد و بدون هیچ گونه دانش قبلی در مورد مجموعه داده ها و دسته های شی و صحنه ، OpponentSIFT توصیه می شود. علاوه بر این ، مجموعه ای ترکیبی از توصیف کننده های رنگ, SIFT مبتنی بر رنگ را بهبود می بخشد و تشخیص دسته را 8 درصد در PASCAL VOC 2007 و 7 درصد در چالش مدیامیل را بهبود می بخشد.
INTRODUCTION
IMAGE category recognition is important to access visual information on the level of objects (buildings, cars, etc.) and scene types (outdoor, vegetation, etc.). In general, systems for category recognition on images [1], [2], [3], [4],[5] and video [6], [7], [8] use machine learning based on image descriptions to distinguish object and scene categories. However, there can be large variations in viewing and lighting conditions for real-world scenes, complicating the description of images and, consequently, the image category recognition task. This is illustrated in Fig. 1. A change in viewpoint will yield shape variations such as the orientation and scale of the object. Salient point detection methods and corresponding region descriptors can robustly detect regions which are translation, rotation, and scale invariant, addressing these viewpoint changes [9], [10], [11]. In addition, changes in the illumination of a scene can greatly affect the performance of object and scene type recognition if the descriptors used are not robust to these changes. To increase photometric invariance and discriminative power, color descriptors have been proposed which are robust against certain photometric changes [12], [13], [14], [15], [16]. As there are many different methods to obtain color descriptors, however, it is unclear what similarities these methods have and how they are different. To arrange color invariant descriptors in the context of image category recognition, a taxonomy is required based on principles of photometric changes.
مقدمه
تشخیص دسته تصویر برای دستیابی به اطلاعات بصری در مورد سطح اشیا ((ساختمانها ، اتومبیل ها و غیره) و انواع صحنه ها (فضای باز ، پوشش گیاهی و غیره) مهم است. به طور کلی ، سیستم های تشخیص دسته بر روی تصاویر [1] ، [2] ، [3] ، [4] ، [5] و ویدئو [6] ، [7] ، [8] از یادگیری ماشین مبتنی بر توصیفات تصویر برای تمایز دسته های شی و صحنه استفاده می کنند. با این وجود ، می توان تنوع زیادی در شرایط مشاهده و روشنایی برای صحنه های دنیای واقعی ایجاد کرد ، که توصیف تصاویر و در نتیجه وظیفه تشخیص دسته تصویر را پیچیده می کند. این در شکل 1 نشان داده شده است. تغییر در دیدگاه تغییرات شکل مانند تغییر در جهت و مقیاس جسم را ایجاد می کند. روش های تشخیص نقطه برجسته و توصیف کننده های منطقه مربوطه می توانند مناطقی را که تبدیل ، چرخش و در مقیاس متفاوت هستند ، به خوبی شناسایی کنند و به این تغییرات دیدگاه در [9] ، [10] ، [11] پرداخته می شود. علاوه بر این ، اگر توصیفگرهای استفاده شده نسبت به این تغییرات مقاوم نباشند تغییر در نور صحنه می تواند تا حد زیادی بر عملکرد تشخیص نوع شی و صحنه تأثیر بگذارد, . برای افزایش مقاومت فتومتریک و قدرت تفکیک ، توصیفگرهای رنگی ارائه شده است که در برابر برخی تغییرات نورسنجی مقاوم هستند [12] ، [13] ، [14] ، [15] ، [16].از آنجا که روشهای مختلفی برای بدست آوردن توصیف رنگ وجود دارد ، معلوم نیست این روشها چه شباهتهایی با هم دارند و تفاوت آنها با یکدیگر چیست. برای مرتب کردن توصیفگرهای مستقل از رنگ در زمینه تشخیص دسته تصویر ، طبقه بندی براساس اصول تغییرات نورسنجی لازم است.
Therefore, this paper studies the invariance properties and the distinctiveness of color descriptors in a structured way. First, a taxonomy of invariant properties is presented. The taxonomy is derived by considering the diagonal model of illumination change [17], [18], [19]. Using this model, a systematic approach is adopted to provide a set of invariance properties which achieve different amounts of invariance, such as invariance to light intensity changes, light intensity shifts, light color changes, and light color changes and shifts. Color descriptors are tested experimentally with respect to this set of invariance properties through an object recognition data set with known illumination changes [20]. Then, the distinctiveness of color descriptors is analyzed experimentally using two benchmarks from the image domain [21] and the video domain [22] . The benchmarks are very different in nature: The image benchmark consists of photographs and the video benchmark consists of keyframes from broadcast news videos. However, they share a common characteristic: Both contain illumination conditions as encountered in the real world. Based on extensive experiments on this large set of real-world image data, the usefulness of the different invariant properties is derived. As a result, new color descriptors can be designed according to the obtained invariance criteria. Finally, recommendations are given on which color descriptors to use under which circumstances and data sets.
بنابراین ، این مقاله خواص عدم تغییر و تمایز توصیف کننده های رنگ را به روشی ساختار یافته بررسی می کند. ابتدا طبقه بندی از خواص ثابت ارائه شده است. طبقه بندی با در نظر گرفتن مدل مورب تغییر روشنایی [17] ، [18] ، [19] بدست می آید. با استفاده از این مدل ، یک رویکرد سیستماتیک اتخاذ می شود تا مجموعه ای از خصوصیات عدم تغییر را به دست آورد که مقادیر مختلفی از عدم تغییر را به دست می آورد ، مانند عدم تغییر در تغییرات شدت نور ، تغییر در جابه جایی نور ، تغییر رنگ و جابه جایی نور. توصیف کننده های رنگ با توجه به این مجموعه از خصوصیات عدم تغییر از طریق مجموعه داده های تشخیص شی با تغییرات روشنایی شناخته شده آزمایش می شوند [20]. سپس ، متمایز بودن توصیفگرهای رنگ با استفاده از دو معیار از دامنه تصویر [21] و دامنه ویدئو [22] به صورت تجربی مورد تجزیه و تحلیل قرار می گیرد.معیارها از نظر ماهیت بسیار متفاوت هستند: معیار تصویر شامل عکس ها و معیار ویدیو شامل فریم های کلیدی از فیلم های خبری پخش شده است. با این حال ، آنها یک ویژگی مشترک دارند: هر دو شامل شرایط نوری هستند که در دنیای واقعی وجود دارد. بر اساس آزمایش های گسترده بر روی این مجموعه بزرگ از داده های تصویر دنیای واقعی ، سودمندی ویژگی های مختلف ثابت از آن بدست آمد. در نتیجه ، توصیفگرهای رنگ جدید می توانند با توجه به معیارهای مستقل از رنگ به دست آمده ، طراحی شوند. سرانجام ، توصیه هایی در مورد توصیف رنگ در کدام شرایط و مجموعه داده ها ارائه می شود.
This paper is organized as follows: In Section 2, the reflectance model is presented. Further, its relation to the diagonal model of illumination change is discussed. In Section 3, a taxonomy of color descriptors and their invariance properties is given. The experimental setup is presented in Section 4. In Section 5, a discussion of the results is given. Finally, in Section 6, conclusions are drawn.
این مقاله به شرح زیر است: در بخش 2 ، مدل بازتاب ارائه شده است. علاوه بر این ، رابطه آن با مدل مورب تغییر روشنایی مورد بحث قرار گرفته است. در بخش 3 ، طبقه بندی توصیف گرهای رنگ و خصوصیات عدم تغییر آنها آورده شده است. تنظیمات آزمایشی در بخش 4 ارائه شده است. در بخش 5 ، بحث در مورد نتایج ارائه شده است. سرانجام ، در بخش 6 ، نتیجه گیری می شود.
REFLECTANCE MODEL
An image f can be modeled under the assumption of Lambertian reflectance as follows. where e(λ) is the color of the light source, s(x,λ) is the surface reflectance, and Pk( λ ) is the camera sensitivity function (k Ԑ {R,G,B}). Further, ω and x are the visible spectrum and the spatial coordinates, respectively.
مدل بازتاب
یک تصویر f را می توان با فرض بازتاب Lambertian به صورت زیر مدلسازی کرد. که در آن e(λ) رنگ منبع نور است ، s(x,λ) بازتابش سطح است و عملکرد Pk( λ ) حساسیت دوربین است (k Ԑ {R,G,B}) . به علاوه، ω و x به ترتیب طیف مرئی و مختصات مکانی هستند.
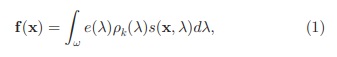
Shafer [23] proposes adding a diffuse term to the model of (1). In fact, the term includes a wider range of possible causes than only diffuse light, such as interreflections, infrared sensitivity of the camera sensor, and scattering in the medium or lens. The diffuse light is considered to have a lower intensity and to originate from all directions in equal amounts. where A(λ) is the term that models the diffuse light.
شفر [23] پیشنهاد می کند یک ترم انتشار(پراکنده) به مدل (1) اضافه شود. در حقیقت ، این ترم دامنه وسیع تری از دلایل احتمالی را شامل می شود که فقط نورمنتشرشده است ، مانند بازتاب ها ، حساسیت مادون قرمز سنسور دوربین و پراکندگی در محیط یا لنز. نوری پراکنده در نظر گرفته می شود که روشنایی کمتری دارد و از همه جهات به مقدار مساوی منشا می گیرد. که در آن A(λ) ترمی است که نور منتشر(پراکنده) را مدل می کند.
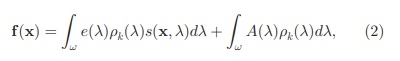
By computing the derivative of image f, it can be easily derived that the effect of a(λ) is canceled out since it is independent of the surface reflectance term. Then, the reflection model of the spatial derivative of f at location x on scale δ is given by:
با محاسبه مشتق تصویر f ، به راحتی می توان نتیجه گرفت که اثر a(λ) لغو می شود زیرا مستقل از ترم بازتاب سطح است. سپس ، مدل بازتاب مشتق مکانی f در مکان x در مقیاسδ توسط رابطه زیر بدست می آید:
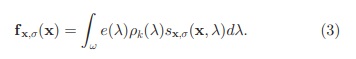
Hence, derivatives will yield invariance to diffuse light. The reflection model of (1) corresponds to the diagonal model of illumination change under the assumption of narrow band filters. This is detailed in the next section.
از این رو ، مشتقات در برابر نورمنتشر شده ، مقاومت(عدم تغییر) نشان می دهند. مدل بازتاب (1) با فرض فیلترهای باند باریک با مدل مورب تغییر روشنایی مطابقت دارد. این در بخش بعدی شرح داده شده است.
Diagonal Model
Changes in the illumination can be modeled by a diagonal mapping or von Kries Model [18] as follows
مدل مورب
تغییرات در روشنایی را می توان با استفاده از نقشه مورب یا مدل von Kries [18] به صورت زیر مدلسازی کرد:

where f^u is the image taken under an unknown light source, f^c is the same image transformed, so it appears as if it was taken under the reference light (called canonical illuminant), and D^u,c is a diagonal matrix which maps colors that are taken under an unknown light source u to their corresponding colors under the canonical illuminant c:
در جایی که f^u تصویری است که تحت یک منبع نوری ناشناخته گرفته می شود ، f^c همان تصویری است که تبدیل شده است ، بنابراین به نظر می رسد که مانند آن در زیر نور مرجع گرفته شده است (روشنایی استاندارد نامیده می شود) ، و D^u,c یک ماتریس مورب است که رنگها را ترسیم می کند تحت یک منبع نوری ناشناخته قرار گرفته و به رنگهای مربوط به آنها در زیر نور متعارف c منتقل می شود:
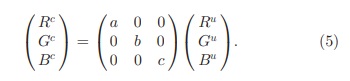
To include the “diffuse” light term, Finlayson et al. [24] extended the diagonal model with an offset (o1; o2; o3)^T , resulting in the diagonal-offset model:
برای شامل کردن ترم نوری “پراکنده” ، Finlayson و همکاران. [24] مدل مورب را با جابجایی o1 گسترش داد. (o1; o2; o3)^T و در نتیجه مدل افست مورب:
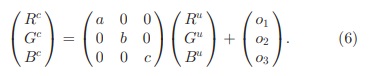
The diagonal model with offset term corresponds to (2) assuming narrow-band filters measured at wavelengths λR, λG, and λB at position x with surface reflectance s(x, λc) as follows:
مدل مورب با ترم آفست مربوط به (2) فرض فیلترهای باند باریک است که در طول موج R ، λ G λ و B λ در موقعیت x با بازتاب سطح s اندازه گیری می شوند. s(x, λc) به شرح زیر است:
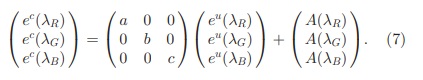
As the surface reflectance sðx; CÞ is equal for both the canonical and the unknown illuminant, (7) is a simplification of
به عنوان بازتاب سطح ؛ s(x, λc) هم برای منبع استاندارد و هم برای منبع نور ناشناخته برابر است ، (7) یک ساده سازی است
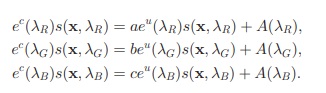
For broad-band cameras, spectral sharpening can be applied to obtain narrow-band filters [17]. Note that similar to (3), when image derivatives are taken (first or higher order image statistics), the offset in the diagonal-offset model will cancel out .
برای دوربینهای باند پهن ، می توان از وضوح طیفی برای بدست آوردن فیلترهای باند باریک استفاده کرد [17]. توجه داشته باشید که مشابه (3) ، هنگامی که مشتقات تصویر گرفته می شوند (آمار تصویر مرتبه اول یا بالاتر) آفست در مدل افست مورب لغو می شود.
Photometric Analysis : Based on the diagonal model and the diagonal-offset model, five types of common changes in the image values f(x) are categorized in this section. First, for (5), when the image values change by a constant factor in all channels (i.e., a =b = c), this is equal to a light intensity change:
تجزیه و تحلیل فوتومتریک
بر اساس مدل مورب و مدل افست مورب ، پنج نوع تغییر متداول در مقادیر تصویر f(x) در این بخش طبقه بندی شده است. اول ، برای (5) ، هنگامی که مقادیر تصویر با یک فاکتور ثابت در همه کانال ها تغییر می کند (به عنوان مثال ، a = b = c) ، این برابر با تغییر شدت نور است:
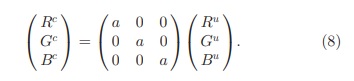
In addition to differences in the intensity of the light source, light intensity changes also include (no-colored) shadows and shading. Hence, when a descriptor is invariant to light intensity changes, it is scale-invariant with respect to (light) intensity .Second, an equal shift in image intensity values in all channels, i.e., light intensity shift, where (o1= o2 = o3) and (a = b = c = 1) will yield:
علاوه بر تفاوت در شدت منبع نور ، تغییرات شدت نور شامل سایه ها ( بدون رنگ) و سایه نیز می شود. از این رو ، وقتی توصیف کننده در تغییرات شدت نور مقاوم است ، از نظر شدت (نور) مستقل از مقیاس است.دوم ، یک تغییر برابر در مقادیر روشنایی تصویر در همه کانال ها ، به عنوان مثال ، تغییر روشنایی نور ، جایی که )o1 = o2 = o3) و (a = b = c = 1(نتیجه می دهد:
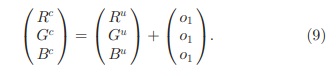
Light intensity shifts are due to diffuse lighting, including scattering of a white light source, object highlights (specular component of the surface) under a white light source, interreflections, and infrared sensitivity of the camera sensor. When a descriptor is invariant to a light intensity shift, it is shift-invariant with respect to light intensity. Third, the above classes of changes can be combined to model both intensity changes and shifts. i.e., an image descriptor robust to these changes is scale invariant and shift-invariant with respect to light intensity.
جابجایی های شدت نور به دلیل روشنایی پراکنده(منتشر شده) ، از جمله پراکندگی یک منبع نور سفید ، هایلایت های جسم (جز خاص سطح) در زیر منبع نور سفید ، بازتاب های متقابل و حساسیت مادون قرمز حسگر دوربین است. هنگامی که توصیف گر در تغییر شدت نور ثابت است ، نسبت به شدت نور تغییر ناپذیر است. سوم ، دسته های تغییرات فوق را می توان برای مدلسازی تغییرات شدت و تغییرات ترکیب کرد. به عنوان مثال ، توصیفگر مقاوم تصویر نسبت به این تغییرات از نظر شدت نور در مقیاس و انتقال ثابت است.
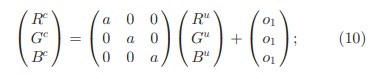
Fourth, in the full diagonal model (i.e., allowing a= b = c), the image channels scale independently (5). This allows for light color changes in the image. Hence, this class of changes can model a change in the illuminant color and light scattering, among others. Finally, the full diagonal-offset model (6) models arbitrary offsets (o1 = o2 = o3), besides the light color changes (a = b = c) offered by the full diagonal model. This type of change is called light color change and shift . In conclusion, five types of common changes have been identified based on the diagonal-offset model of illumination change, i.e., variations to light intensity changes, light intensity shifts, light intensity changes and shifts, light color changes, and light color changes and shifts.
چهارم ، در مدل مورب کامل (یعنی اجازه دادن a= b = c ) ، کانال های تصویر به طور مستقل مقیاس می شوند (5) این امکان را برای تغییر رنگ نور در تصویر فراهم می کند. از این رو ، این دسته از تغییرات می توانند تغییر در رنگ روشنایی و پراکندگی نور را با هم مدل کنند. سرانجام ، مدل افست مورب کامل (6) علاوه بر تغییر رنگ نور ( a= b= c) که توسط مدل کامل مورب ارائه می شود ، آفست دلخواه (o1 = o2 = o3) را ارائه می دهد. این نوع تغییر را تغییر و انتقال روشنایی رنگ می نامند. در نتیجه ، پنج نوع تغییرات مشترک بر اساس مدل آفست مورب از تغییر روشنایی ، یعنی تغییرات شدت نور ، انتقال روشنایی نور ، تغییرات و انتقال روشنایی نور ، تغییرات رنگ نور و و تغییر و انتفال رنگ نور شناسایی شده است.
COLOR DESCRIPTORS AND INVARIANT PROPERTIES
In this section, color descriptors are presented and their invariance properties are summarized. First, color descriptors based on histograms are discussed. Then, color moments and color moment invariants are presented. Finally, color descriptors based on SIFT are discussed. These three types of descriptors were chosen due to their distinct nature and wide-spread use. Color histograms do not contain local spatial information and are inherently pixel-based. Color moments do contain local photometrical and spatial information derived from pixel values. SIFT descriptors contain local spatial information and are derivative-based.
توصیف گرهای رنگ و ویژگی های ثابت
در این بخش ، توصیفگرهای رنگی ارائه شده و خصوصیات نامتغیر آنها خلاصه می شود. در ابتدا ، توصیفگرهای رنگ بر اساس هیستوگرام بحث شده است. سپس ، گشتاورهای رنگی و گشتاورهای نامتغیر رنگ ارائه می شوند. سرانجام ، توصیفگرهای رنگ بر اساس SIFT مورد بحث قرار گرفته است. این سه نوع توصیفگر به دلیل ماهیت مجزا و کاربرد گسترده آنها انتخاب شده اند. هیستوگرام های رنگی حاوی اطلاعات مکانی محلی نیستند و ذاتاً مبتنی بر پیکسل هستند. گشتاورهای رنگی حاوی اطلاعات فوتومتریک محلی و مکانی ناشی از مقادیر پیکسل هستند. توصیف کننده های SIFT حاوی اطلاعات مکانی محلی هستند و مبتنی بر مشتقات هستند.
See Table 1 for an overview of the descriptors and their invariance properties. We define invariance of a descriptor to condition A as follows: Under a condition A, the descriptor is independent of changes in condition A. The independence is derived analytically under the assumption that no color clipping occurs. Color clipping occurs when the color of a pixel falls outside the valid range and is subsequently clipped to the minimum or maximum of the range. For example, for a very large scaling of the intensity in (8), color clipping occurs if the scaled values exceed 255, the maximum value typically used for image storage
برای مروری بر توصیفگرها و خصوصیات نامتغیر آنها به جدول 1 مراجعه کنید. ما مقاومت توصیف گر در شرط A را به شرح زیر تعریف می کنیم: تحت شرایط A ، توصیفگرمستقل از تغییر در شرایط A است. استقلال از نظر تحلیلی با این فرض که هیچ بریدگی رنگی اتفاق نمی افتد ، بدست می آید. قطع رنگ زمانی اتفاق می افتد که رنگ پیکسل خارج از محدوده معتبر باشد و متعاقباً به حداقل یا حداکثر دامنه بریده شود. به عنوان مثال ، برای مقیاس های بسیار بزرگ روشنایی (8) ، اگر مقادیر مقیاس از 255 بیشتر شود ، حداکثر مقدار که معمولاً برای ذخیره سازی تصویر استفاده می شود به این صورت قطع رنگ رخ می دهد
Histograms
RGB histogram. The RGB histogram is a combination of three 1D histograms based on the R, G, and B channels of the RGB color space. This histogram possesses no invariance properties.
Opponent histogram. The opponent histogram is a combination of three 1D histograms based on the channels of the opponent color space:
3.1 هیستوگرام
هیستوگرام RGB. هیستوگرام RGB ترکیبی از سه هیستوگرام 1D بر اساس کانال های R ، G و B فضای رنگی RGB است. این هیستوگرام هیچ خاصیت عدم تغییر ندارد.
هیستوگرام مخالف(Opponent). هیستوگرام مخالف ترکیبی از سه هیستوگرام 1D بر اساس کانالهای فضای رنگ مخالف است
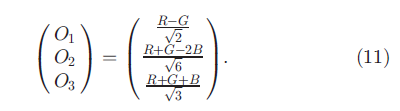
The intensity information is represented by channel O3 and the color information by O1 and O2. Due to the subtraction in O1 and O2, the offsets will cancel out if they are equal for all channels (e.g., a white light source). This is verified by substituting the unknown illuminant from (9) with offset o1 Therefore, these O1 and O2 are shift-invariant with respect to light intensity. The intensity channel O3 has no invariance properties
اطلاعات روشنایی توسط کانال O3 و اطلاعات رنگ توسط O1 و O2 نشان داده می شود. به دلیل تفریق در O1 و O2 ، اگر برای همه کانال ها برابر باشد ، خنثی می شود (مثلاً یک منبع نور سفید). این با جایگزینی روشن کننده ناشناخته از (9) با آفست o1 تأیید می شود. بنابراین ، این O1 و O2 با توجه به شدت نور ، نسبت به انتقال تغییر ناپذیر هستند. کانال روشنایی O3 هیچ خاصیت نامتغیر ندارد .

Hue histogram. In the HSV color space, it is known that the hue becomes unstable near the gray axis. To this end, van de Weijer et al. [14] apply an error propagation analysis to the hue transformation. The analysis shows that the certainty of the hue is inversely proportional to the saturation. Therefore, the hue histogram is made more robust by weighing each sample of the hue by its saturation. The H color model is scale-invariant and shift-invariant with respect to light intensity [14].
هیستوگرام Hue. در فضای رنگی HSV مشخص شده است که در نزدیکی محور خاکستری, رنگ ناپایدار می شود. به همین منظور ، ون دی ویجر و همکاران. [14] تجزیه و تحلیل انتشار خطا را برای تبدیل رنگ به کار گرفتند. تجزیه و تحلیل نشان می دهد که اطمینان از رنگ متناسب با معکوس اشباع است. بنابراین ، با وزندهی به هر نمونه از رنگ با اشباع ، هیستوگرام رنگ قوی تر می شود. مدل رنگ H با توجه به شدت نور ،در مقیاس و انتقال تغییر ناپذیر است [14].
rghistogram. In the normalized RGB color model, the chromaticity components r and g describe the color information in the image (b is redundant as r + g + b= 1):
rghistogram. در مدل رنگی RGB نرمال شده ، کیفیت اجزای رنگی r و g اطلاعات رنگی در تصویر را توصیف می کنند (b در r + g+ b = 1 زائد است):
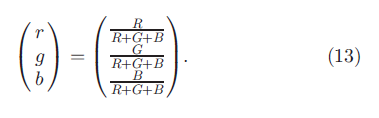
Because of the normalization, r and g are scale-invariant, and thereby invariant to light intensity changes, shadows, and shading [25] from (8):
به دلیل نرمالیزه شدن ، r و g در مقیاس ثابت هستند ، و در نتیجه در تغییرات شدت نور ، سایه ها و shading تغییر نمی کنند [25] از (8):
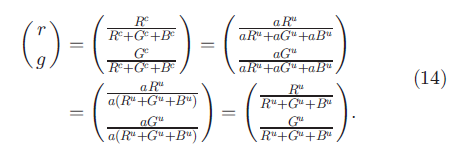
Transformed color distribution. An RGB histogram is not invariant to changes in lighting conditions. However, by normalizing the pixel value distributions, scale-invariance and shift-invariance is achieved with respect to light intensity. Because each channel is normalized independently, the descriptor is also normalized against changes in light color and arbitrary offsets:
توزیع رنگ تبدیل شده . هیستوگرام RGB با تغییر در شرایط نوری ثابت نیست. با این حال ، با نرمال سازی توزیع های مقدار پیکسل ، عدم تغییر مقیاس و انتقال از نظر شدت نور حاصل می شود. از آنجا که هر کانال به طور مستقل نرمال می شود ، توصیف گر نیز در برابر تغییرات در رنگ روشن و آنحراف خودسرانه نرمال می شود:
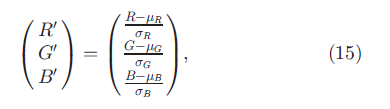
with μc the mean and δc the standard deviation of the distribution in channel C computed over the area under consideration (e.g., a patch or image). This yields, for every channel, a distribution where μ = 0 and δ = 1.
با μc میانگین و δc انحراف معیار توزیع در کانال C در منطقه مورد نظر محاسبه شده است (به عنوان مثال ، یک پچ یا تصویر). این به ازای هر کانال توزیعی است که میانگین برابر 0 و انحراف معیار برابر 1, نتیجه می دهد.
Color Moments and Moment Invariants
A color image corresponds to a function I defining RGB triplets for image positions (x,y):I:(x,y)—(R(x,y), G(x,y),B(x,y)) By regarding RGB triplets as data points coming from a distribution, it is possible to define moments. Mindru et al. [26] have defined generalized color moments M:
گشتاورهای رنگی و گشتاورهای ثابت
یک تصویر رنگی مربوط به تابعی است که من برای تعیین موقعیت های تصویر سه گانه RGB تعریف می کنم. (x,y):I:(x,y)—(R(x,y), G(x,y),B(x,y)) ؛ با در نظر گرفتن سه گانه های RGB به عنوان نقاط داده ای که از یک توزیع به دست می آیند ، می توان گشتاورها را تعریف کرد. میندرو و همکاران [26] گشتاورهای رنگ تعمیم یافته را تعریف کرده اند :
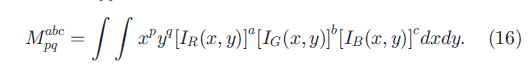
M is referred to as a generalized color moment of order ( p + q) and degree (a + b + c). Note that moments of order 0 do not contain any spatial information, while moments of degree 0 do not contain any photometric information. Thus, moment descriptions of order 0 are rotationally invariant, while higher orders are not. A large number of moments can be created with small values for the order and degree. However, for larger values the moments are less stable. Typically, generalized color moments up to the first order and the second degree are used. By using the proper combination of moments, it is possible to normalize against photometric changes. These combinations are called color moment invariants. Invariants involving only a single color channel (e.g., out of a, b, and c two are 0) are called 1-band invariants. Similarly, there are 2-band invariants involving only two out of three color bands. 3-band invariants involve all color channels, but these can always be created by using 2-band invariants for different combinations of channels.
از M به عنوان یک گشتاور رنگی تعمیم یافته از مرتبه p + q و درجه a + b + c یاد می شود. توجه داشته باشید که گشتاور از مرتبه 0 هیچ اطلاعات مکانی را ندارند ، و گشتاورهای از درجه 0 هیچ اطلاعات فوتومتریک را ندارند. بنابراین ، توصیف گشتاور مرتبه 0 از نظر چرخشی ثابت است ، در حالی که درجه های بالاتر اینگونه نیست. تعداد زیادی گشتاورها را می توان با مقادیر کوچک برای مرتبه و درجه ایجاد کرد. با این حال ، برای مقادیر بزرگتر ، گشتاور ها کم ترپایدارهستند. به طور معمول ، از گشتاورهای رنگی تعمیم یافته تا درجه اول و درجه دوم استفاده می شود. با استفاده از ترکیب مناسب گشتاورها ، می توان در برابر تغییرات نورسنجی آن ها را نرمال سازی کرد. به این ترکیبات گشتاورهای مقاوم رنگ گفته می شود. عواملی که فقط شامل یک کانال تک رنگ هستند (به عنوان مثال ، از a ، b و c دو عدد 0 هستند) 1 بانده می نامند. به همین ترتیب ، 2 باندهای ثابت وجود دارد که از هر سه باند رنگ فقط دو مورد را شامل می شود. نامتغییرهای 3 باند شامل همه کانالهای رنگی هستند ، اما اینها همیشه با استفاده از نامتغیرهای 2 بانده برای ترکیبات مختلف کانال ایجاد می شوند.
Color moments. The color moment descriptor uses all generalized color moments up to the second degree and the first order. This leads to nine possible combinations for the degree: xxxx Combined with three possible combinations for the order, xxx , the color moment descriptor has 27 dimensions. These color moments only have shift-invariance. This is achieved by subtracting the average in all input channels before computing the moments.
گشتاور های رنگی .توصیفگر گشتاور رنگ از تمام گشتاور های رنگی تعمیم یافته تا درجه دوم و مرتبه اول استفاده می کند. این به 9 ترکیب ممکن برای درجه منجر می شود: xxx همراه با سه ترکیب ممکن برای مرتبه ، xxxx ، توصیف کننده گشتاور رنگ دارای 27 بعد است. این گشتاورها رنگی فقط نسبت به انتقال تغییر ناپذیری دارند. این امر با کسر میانگین در کلیه کانالهای ورودی قبل از محاسبه گشتاورها حاصل می شود.
Color moment invariants. Color moment invariants can be constructed from generalized color moments. All 3-band invariants are computed from Mindru et al. [26]. To be comparable, the C02 invariants are considered. This gives a total of 24 color moment invariants, which are invariant to all the properties listed in Table 1.
گشتاورهای مقاوم رنگ. گشتاورهای مقاوم رنگ را می توان ازگشتاور های رنگی تعمیم یافته ساخت. همه موارد ثابت 3 باند از Mindru و همکاران محاسبه می شود. [26] برای مقایسه ، موارد C02 در نظر گرفته می شوند. این در مجموع 24 گشتاور رنگی مقاوم به دست می دهد ، که در تمام خصوصیات ذکر شده در جدول 1 ثابت هستند.
Color SIFT Descriptors
SIFT. The SIFT descriptor proposed by Lowe [9] describes the local shape of a region using edge orientation histograms. The gradient of an image is shift-invariant: taking the derivative cancels out offsets (Section 2.2). Under light intensity changes, i.e., a scaling of the intensity channel, the gradient direction and the relative gradient magnitude remain the same. Because the SIFT descriptor is normalized, the gradient magnitude changes have no effect on the final descriptor. The SIFT descriptor is not invariant to light color changes because the intensity channel is a combination of the R, G, and B channels. To compute SIFT descriptors, the version described by Lowe [9] is used
توصیفگر رنگ SIFT
توصیفگر SIFT که توسط لو [9] پیشنهاد شده است ، شکل محلی یک منطقه را با استفاده از هیستوگرام های جهت گیری لبه توصیف می کند. شیب یک تصویر تغییر ناپذیر است: گرفتن مشتق باعث لغو انحراف ها (بخش 2.2). تحت تغییرات شدت نور ، به عنوان مثال ، مقیاس شدت کانال، جهت گرادیان و اندازه گرادیان نسبی ثابت می مانند. از آنجا که توصیفگر SIFT نرمال است ، تغییرات اندازه گرادیان تأثیری بر توصیف کننده نهایی ندارد. توصیفگر SIFT در تغییر رنگ نور مقاوم نیست زیرا کانال رنگ ترکیبی از کانالهای R ، G و B است. برای محاسبه توصیفگرهای SIFT ، از نسخه توصیف شده توسط لو [9] استفاده شده است
HSV-SIFT. Bosch et al. [16] compute SIFT descriptors over all three channels of the HSV color model. This gives 3 * 128 dimensions per descriptor, 128 per channel. As stated earlier, the H color model is scale-invariant and shift invariant with respect to light intensity. However, due to the combination of the HSV channels, the complete descriptor has no invariance properties. Further, the instability of the hue for low saturation is not addressed here.
HSV-SIFT. بوش و همکاران [16] توصیفگرهای SIFT را در هر سه کانال مدل رنگی HSV محاسبه شود . این به ازای هر توصیفگر 3/ 128 واحد ، در هر کانال 128 بعد می دهد. همانطور که قبلاً بیان شد ، مدل رنگ H با توجه به شدت نور ،نسبت به مقیاس و انتقال ثابت است. با این حال ، به دلیل ترکیب کانال های HSV ، توصیف گر کامل هیچ خاصیت عدم تغییر ندارد. بعلاوه ، در اینجا به بی ثباتی رنگ برای اشباع کم پرداخته نشده است.
HueSIFT. Van de Weijer et al. [14] introduce a concatenation of the hue histogram (see Section 3.1) with the SIFT descriptor. When compared to HSV-SIFT, the usage of the weighed hue histogram addresses the instability of the hue near the gray axis. Because the bins of the hue histogram are independent, the periodicity of the hue channel for HueSIFT is addressed. Similar to the hue histogram, the HueSIFT descriptor is scale-invariant and shift-invariant.
HueSIFT. وان دی ویجر و همکاران [14] الحاق هیستوگرام رنگ (به بخش 3.1 مراجعه کنید) با توصیفگر SIFT را معرفی می کند. وقتی با HSV-SIFT مقایسه می شود ، استفاده ازهیستوگرام رنگ توزین شده به ناپایداری رنگ در نزدیکی محور خاکستری می پردازد. از آنجا که بین های سطوح هیستوگرام رنگ مستقل هستند ، به تناوب کانال رنگ برای HueSIFT پرداخته می شود. مشابه هیستوگرام رنگ ، توصیفگر HueSIFT مقیاس ثابت و تغییر ناپذیر است.
OpponentSIFT. OpponentSIFT describes all of the channels in the opponent color space (11) using SIFT descriptors. The information in the O3 channel is equal to the intensity information, while the other channels describe the color information in the image. These other channels do contain some intensity information, but, due to the normalization of the SIFT descriptor, they are invariant to changes in light intensity.
SIFT. OpponentSIFT با استفاده از توصیفگرهای SIFT همه کانالهای موجود در فضای رنگ حریف (11) را توصیف می کند. اطلاعات موجود در کانال O3 با اطلاعات روشنایی برابر است ، در حالی که کانالهای دیگر اطلاعات رنگی را در تصویر توصیف می کنند. این کانالهای دیگر حاوی برخی از اطلاعات روشنایی هستند ، اما ، به دلیل نرمال شدن توصیفگر SIFT ، در تغییرات شدت نور ثابت هستند.
C-SIFT. In the opponent color space, the O1 and O2 channels still contain some intensity information. To add invariance to intensity changes, [13] proposes the C-invariant, which eliminates the remaining intensity information from these channels. The use of color invariants as input for SIFT was first suggested by Abdel-Hakim and Farag [12]. The C-SIFT descriptor [15] uses the C-invariant, which can be intuitively seen as the normalized opponent color space O1O3and O2O3. Because of the division by intensity,the scaling in the diagonal model will cancel out, making C-SIFT scale-invariant with respect to light intensity. Due to the definition of the color space, the offset does not cancel out when taking the derivative: It is not shift-invariant.
C-SIFT :در فضای رنگی حریف ، کانالهای O1 و O2 هنوز حاوی برخی اطلاعات روشنایی هستند. [13] برای افزودن ثبات دربرابر تغییرات روشنایی ، C-invariant را پیشنهاد می کند که اطلاعات روشنایی باقی مانده را از این کانال ها حذف می کند. استفاده از موارد نامتغیر به عنوان ورودی برای SIFT اولین بار توسط عبدالحکیم و فراگ پیشنهاد شد [12]. توصیفگر C-SIFT [15] از C-invariant استفاده می کند ، که می توان بصورت شهودی آن را به عنوان فضای رنگی مخالف نرمال O1O3 و O2O3 مشاهده کرد. به دلیل تقسیم برروشنایی ، مقیاس در مدل مورب از بین می رود و مقیاس C-SIFT را با توجه به شدت نور تغییر نمی دهد. با توجه به تعریف فضای رنگ ، آفست هنگام استفاده از مشتق لغو نمی شود:پس تغییر ناپذیر نیست.
rgSIFT. For the rgSIFT descriptor, descriptors are added for the r and g chromaticity components of the normalized RGB color model from (13), which is already scale-invariant.
rgSIFT. برای توصیفگر rgSIFT ، توصیفگرها برای اجزای رنگی r و g مدل رنگی RGB نرمال شده از (13) اضافه می شوند ، که از قبل نسبت به مقیاس ثابت است.
Transformed color SIFT. For the transformed color SIFT, the same normalization is applied to the RGB channels as for the transformed color histogram (15). For every normalized channel, the SIFT descriptor is computed. The descriptor is scale-invariant, shift-invariant, and invariant to light color changes and shift.
SIFT تبدیل شده رنگی . برای SIFT رنگی تبدیل شده ، همان نرمال کردن برای کانالهای RGB اعمال می شود که برای هیستوگرام رنگ تبدیل شده (15). برای هر کانال نرمال شده ، توصیفگر SIFT محاسبه می شود. توصیف گر در انتقال و تغییر رنگ نور ، مقیاس ثابت است.
RGB-SIFT. For the RGB-SIFT descriptor, SIFT descriptors are computed for every RGB channel independently An interesting property of this descriptor is that its descriptor values are equal to the transformed color SIFT descriptor. This is explained by looking at the transformed color space (15): This transformation is already implicitly performed when SIFT is applied to each RGB channel independently. Because the SIFT descriptor operates on derivatives only, the subtraction of the means in the transformed color model is redudant as this offset is already canceled out by taking derivatives. Similarly, the division by the standard deviation is already implicitly performed by the normalization of the vector length of SIFT descriptors. Therefore, as the RGB-SIFT and transformed color SIFT descriptors are equal, we will use the RGB-SIFT name throughout this paper.
RGB-SIFT .برای توصیفگر RGB-SIFT ، توصیفگرهای SIFT برای هر کانال RGB به طور مستقل محاسبه می شوندویژگی جالب این توصیفگر این است که مقادیر توصیف کننده آن برابر با توصیف کننده رنگ تبدیل شده SIFT است. این امر با مشاهده فضای رنگی تبدیل یافته توضیح داده می شود: (15):این تبدیل قبلا به طور ضمنی انجام شده است زمانی که به طور مستقل بر روی هر کانال RGB عمل می کند.زیرا توصیفگر SIFT فقط بر روی مشتقات عمل می کند ، تفریق میانگین در مدل رنگی تبدیل شده از بین می رود زیرا این آفست با استفاده از مشتقات قبلاً لغو شده است. به طور مشابه ، تقسیم بر اساس انحراف معیار در حال حاضر به طور ضمنی توسط نرمال سازی طول بردار توصیف گرهای SIFT انجام می شود. بنابراین ، از آنجا که توصیف کنندگان RGB-SIFT و SIFT رنگی تبدیل شده برابر هستند ، ما از نام RGB-SIFT در کل این مقاله استفاده خواهیم کرد.
Conclusion
In this section, three different groups of color descriptors were discussed: histograms in different color spaces, color moments, and moment invariants and color extensions of SIFT. For each color descriptor, the invariance with respect to illumination changes in the diagonal-offset model were analyzed. The results are summarized in Table 1.
نتیجه گیری
در این بخش ، سه گروه مختلف از توصیف کننده های رنگ مورد بحث قرار گرفتند: هیستوگرام در فضاهای رنگی مختلف ، گشتاورهای رنگی ، و تغییرات گشتاور و گسترش های رنگی SIFT. برای هر توصیف کننده رنگ ، عدم تغییر با توجه به تغییرات روشنایی در مدل افست مورب مورد تجزیه و تحلیل قرار گرفت. نتایج در جدول 1 خلاصه شده است.
