آموزش یک شبکه عصبی متراکم ساده بینایی ماشین برای تشخیص اعداد دست نویس در پایتورچ
آگوست 24, 2023آموزش شبکه عصبی کانولوشن چند لایه در پایتورچ برای طبقه بندی تصویر
آگوست 26, 2023استفاده از شبکه عصبی کانولوشنال برای طبقه بندی ارقام دست نویس در پایتورچ
در نوشته قبلی یاد گرفتیم که چگونه یک شبکه عصبی چند لایه را با استفاده از تعریف کلاس تعریف کنیم، اما این شبکهها عمومی بودند و برای وظایف بینایی کامپیوتری تخصصی نبودند. در این بخش با شبکه های عصبی کانولوشن (CNN) آشنا می شویم که به طور خاص برای بینایی کامپیوتری طراحی شده اند.
بینایی کامپیوتری با طبقهبندی عمومی متفاوت است، زیرا زمانی که ما در تلاش برای یافتن یک شی خاص در تصویر هستیم، تصویر را اسکن میکنیم و به دنبال الگوهای خاص و ترکیب آنها هستیم. به عنوان مثال، هنگامی که به دنبال گربه می گردیم، ابتدا ممکن است به دنبال خطوط افقی باشیم که می توانند سبیل ها را تشکیل دهند و سپس ترکیب خاصی از سبیل ها می تواند به ما بگوید که در واقع تصویر یک گربه است. موقعیت نسبی و حضور الگوهای خاص مهم است و نه موقعیت دقیق آنها روی تصویر.
برای استخراج الگوها، از مفهوم فیلترهای کانولوشنال استفاده می کنیم. اما ابتدا اجازه دهید تمام وابستگی ها و توابعی را که در واحدهای قبلی تعریف کرده ایم بارگذاری کنیم.
!wget https://raw.githubusercontent.com/MicrosoftDocs/pytorchfundamentals/main/computer-vision-pytorch/pytorchcv.py
import torch
import torch.nn as nn
import torchvision
import matplotlib.pyplot as plt
from torchinfo import summary
import numpy as np
from pytorchcv import load_mnist, train, plot_results, plot_convolution, display_dataset
load_mnist(batch_size=128)
فیلترهای کانولوشنال
فیلترهای کانولوشن پنجره های کوچکی هستند که روی هر پیکسل تصویر اجرا می شوند و میانگین وزنی پیکسل های مجاور را محاسبه می کنند.
کشویی پنجره روی تصویر 28×28 رقمی
آنها با ماتریس های ضرایب وزنی تعریف می شوند. بیایید نمونههای اعمال دو فیلتر کانولوشنال مختلف را روی ارقام دستنویس MNIST خود ببینیم.
plot_convolution(torch.tensor([[-1.,0.,1.],[-1.,0.,1.],[-1.,0.,1.]]),'Vertical edge filter')
plot_convolution(torch.tensor([[-1.,-1.,-1.],[0.,0.,0.],[1.,1.,1.]]),'Horizontal edge filter')
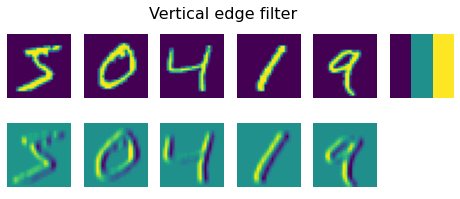
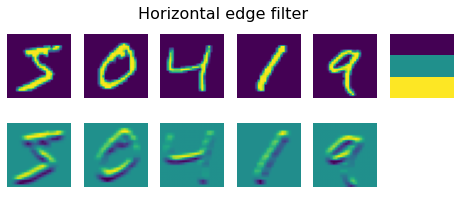
فیلتر اول، فیلتر لبه عمودی نامیده می شود و با ماتریس زیر تعریف می شود:
−1−1−1000111
هنگامی که این فیلتر روی یک میدان پیکسل نسبتا یکنواخت می رود، همه مقادیر به 0 می رسد. اما، هنگامی که با یک لبه عمودی در تصویر مواجه می شود، مقدار تیزی بالایی ایجاد می شود. به همین دلیل است که در تصاویر بالا میتوانید لبههای عمودی را مشاهده کنید که با مقادیر بالا و پایین نشان داده شدهاند، در حالی که لبههای افقی بهطور میانگین نشان داده شدهاند.
هنگامی که فیلتر لبه افقی را اعمال می کنیم، یک چیز برعکس اتفاق می افتد – خطوط افقی تقویت می شوند، و عمودی به طور متوسط از بین می روند.
اگر فیلتر 3×3 را روی تصویری با اندازه 28×28 اعمال کنیم – اندازه تصویر 26×26 می شود، زیرا فیلتر از مرزهای تصویر فراتر نمی رود. با این حال، در برخی موارد، ممکن است بخواهیم اندازه تصویر را ثابت نگه داریم، در این صورت تصویر با صفر در هر طرف پر می شود.
در بینایی کامپیوتری کلاسیک، چندین فیلتر برای تولید ویژگیها روی تصویر اعمال میشد سپس توسط الگوریتم یادگیری ماشین برای ساخت یک طبقهبندی کننده استفاده میشد. با این حال، در یادگیری عمیق، شبکههایی میسازیم که بهترین فیلترهای کانولوشنال را برای حل مسئله طبقهبندی میآموزند.
برای انجام این کار، لایه های کانولوشن را معرفی می کنیم.
لایه های کانولوشن
لایه های کانولوشن با استفاده از ساختار nn.Conv2d تعریف می شوند. باید موارد زیر را مشخص کنیم:
in_channels – تعداد کانال های ورودی. در مورد ما با یک تصویر در مقیاس خاکستری سروکار داریم، بنابراین تعداد کانال های ورودی 1 است. تصویر رنگی دارای 3 کانال (RGB) است.
out_channels – تعداد فیلترهای مورد استفاده. ما از 9 فیلتر مختلف استفاده خواهیم کرد که به شبکه فرصت های زیادی می دهد تا ببیند کدام فیلتر برای سناریوی ما بهتر عمل می کند.
kernel_size اندازه پنجره کشویی است. معمولا از فیلترهای 3×3 یا 5×5 استفاده می شود. انتخاب اندازه فیلتر معمولاً با آزمایش انتخاب می شود، یعنی با آزمایش اندازه های مختلف فیلتر و مقایسه دقت حاصل.
ساده ترین CNN دارای یک لایه کانولوشن است. با توجه به اندازه ورودی 28×28، پس از اعمال نه فیلتر 5×5، به یک تانسور 9x24x24 خواهیم رسید (اندازه فضایی کوچکتر است، زیرا تنها در 24 موقعیت وجود دارد که فاصله به طول 5 می تواند در 28 پیکسل قرار گیرد). در اینجا نتیجه هر فیلتر با یک کانال متفاوت در تصویر نشان داده می شود (بنابراین بعد اول 9 مربوط به تعداد فیلترها است).
پس از کانولوشن، تانسور 9x24x24 را در یک بردار به اندازه 5184 flatten می کنیم و سپس لایه خطی را اضافه می کنیم تا 10 کلاس تولید شود. ما همچنین از تابع فعال سازی relu در بین لایه ها استفاده می کنیم.
class OneConv(nn.Module):
def __init__(self):
super(OneConv, self).__init__()
self.conv = nn.Conv2d(in_channels=1,out_channels=9,kernel_size=(5,5))
self.flatten = nn.Flatten()
self.fc = nn.Linear(5184,10)
def forward(self, x):
x = nn.functional.relu(self.conv(x))
x = self.flatten(x)
x = nn.functional.log_softmax(self.fc(x),dim=1)
return x
net = OneConv()
summary(net,input_size=(1,1,28,28))
==========================================================================================
Layer (type:depth-idx) Output Shape Param #
==========================================================================================
├─Conv2d: 1-1 [1, 9, 24, 24] 234
├─Flatten: 1-2 [1, 5184] --
├─Linear: 1-3 [1, 10] 51,850
==========================================================================================
Total params: 52,084
Trainable params: 52,084
Non-trainable params: 0
Total mult-adds (M): 0.18
==========================================================================================
Input size (MB): 0.00
Forward/backward pass size (MB): 0.04
Params size (MB): 0.21
Estimated Total Size (MB): 0.25
==========================================================================================
می بینید که این شبکه حاوی حدود 50k پارامتر قابل آموزش است، در مقایسه با حدود 80k در شبکه های چند لایه کاملاً متصل. این به ما امکان می دهد حتی در مجموعه داده های کوچکتر به نتایج خوبی دست یابیم، زیرا شبکه های کانولوشنی بسیار بهتر تعمیم می یابند.
توجه داشته باشید که تعداد پارامترهای لایه کانولوشن بسیار کم است و به وضوح تصویر بستگی ندارد! در مورد ما از 9 فیلتر با ابعاد 5×5 استفاده کردیم، بنابراین تعداد پارامترها 9×5×5+9=234 است. اگرچه در بحث بالا این مورد را از دست دادیم، اما فیلتر کانولوشنال نیز بایاس دارد. بیشتر پارامترهای شبکه ما از لایه نهایی Dense می آید.
hist = train(net,train_loader,test_loader,epochs=5)
plot_results(hist)
Epoch 0, Train acc=0.947, Val acc=0.969, Train loss=0.001, Val loss=0.001
Epoch 1, Train acc=0.979, Val acc=0.975, Train loss=0.001, Val loss=0.001
Epoch 2, Train acc=0.985, Val acc=0.977, Train loss=0.000, Val loss=0.001
Epoch 3, Train acc=0.988, Val acc=0.975, Train loss=0.000, Val loss=0.001
Epoch 4, Train acc=0.988, Val acc=0.976, Train loss=0.000, Val loss=0.001
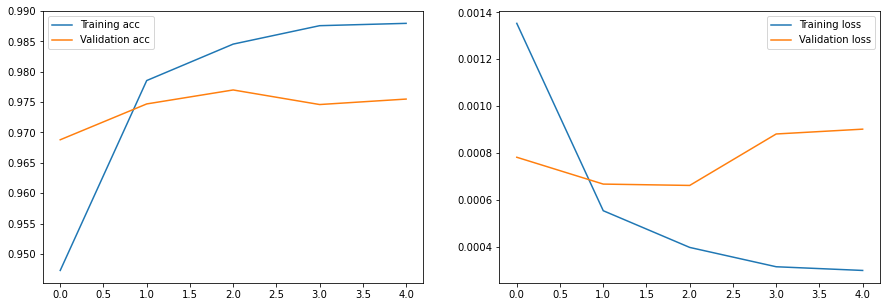
همانطور که می بینید، در مقایسه با شبکه های کاملا متصل نوشته قبلی، می توانیم به دقت بالاتر و بسیار سریعتر دست یابیم.
ما همچنین میتوانیم وزن لایههای کانولوشنال آموزشدیده خود را نمایش دهیم، تا درک بیشتری از آنچه در حال وقوع است داشته باشیم:
fig,ax = plt.subplots(1,9)
with torch.no_grad():
p = next(net.conv.parameters())
for i,x in enumerate(p):
ax[i].imshow(x.detach().cpu()[0,...])
ax[i].axis('off')

می بینید که برخی از این فیلترها به نظر می رسد که می توانند برخی از لبه و خطوط های مورب را تشخیص دهند، در حالی که برخی دیگر بسیار تصادفی به نظر می رسند.
بردن
لایه کانولوشن به ما امکان می دهد الگوهای تصویر خاصی را از تصویر استخراج کنیم، به طوری که طبقه بندی نهایی بر اساس آن ویژگی ها باشد. با این حال، میتوانیم از همان رویکرد استخراج الگوها در داخل فضای ویژگی، با چیدن یک لایه کانولوشنال دیگر در بالای لایه اول استفاده کنیم. در بخش بعدی با شبکه های کانولوشن چندلایه آشنا خواهیم شد.
