الگوریتم K-نزدیکترین همسایه (KNN)
دسامبر 4, 2022شبکه عمیق برای تصاویر سنجش دور
مارس 28, 2023الگوریتم EM (Expectation-Maximization)
در بسیاری از بیان مسئله واقعی یادگیری ماشین، بسیار رایج است که ما ویژگیهای مرتبط زیادی برای ساخت مدل خود در دسترس داریم، اما تنها بخش کوچکی از آنها قابل مشاهده است. از آنجایی که ما مقادیر متغیرهای مشاهده نشده (مخفی) را نداریم، الگوریتم Expectation-Maximization سعی می کند از داده های موجود برای تعیین مقادیر بهینه برای این متغیرها استفاده کند و سپس پارامترهای مدل را پیدا کند.
فهرست مطالب
👉 الگوریتم انتظار-بیشینه سازی (EM) چیست؟
👉 توضیح دقیق الگوریتم EM
👉 نمودار جریان
👉 مزایا و معایب
👉 کاربردهای الگوریتم EM
👉 از الگوریتم EM استفاده کنید
مقدمه ای بر توزیع های گاوسی
مدلهای مخلوط گاوسی (GMM)
👉 پیاده سازی مدل های مخلوط گاوسی در پایتون
الگوریتم انتظار-بیشینه سازی (EM) چیست؟
یک مدل متغیر پنهان است.
بیایید ابتدا بفهمیم که منظور از مدل متغیر پنهان چیست؟
یک مدل متغیر پنهان از متغیرهای قابل مشاهده همراه با متغیرهای غیرقابل مشاهده تشکیل شده است. متغیرهای مشاهده شده آن دسته از متغیرهای مجموعه داده هستند که می توانند اندازه گیری شوند در حالی که متغیرهای مشاهده نشده (مخفی/پنهان) از متغیرهای مشاهده شده استنباط می شوند.
👉 می توان از آن برای یافتن پارامترهای حداکثربیشینه درستنمایی (MLE) یا حداکثر پارامترهای پسینی (MAP) برای متغیرهای پنهان استفاده کرد.
در یک مدل آماری یا ریاضی.
👉 برای پیشبینی این مقادیر گمشده در مجموعه داده استفاده میشود، مشروط بر اینکه شکل کلی توزیع احتمال مرتبط با این متغیرهای پنهان را بدانیم.
👉 به عبارت ساده، ایده اصلی پشت این الگوریتم استفاده از نمونه های قابل مشاهده متغیرهای پنهان برای پیش بینی مقادیر نمونه هایی است که برای یادگیری غیر قابل مشاهده هستند. این فرآیند تا زمانی که همگرایی مقادیر اتفاق بیفتد تکرار می شود.
توضیح دقیق الگوریتم EM
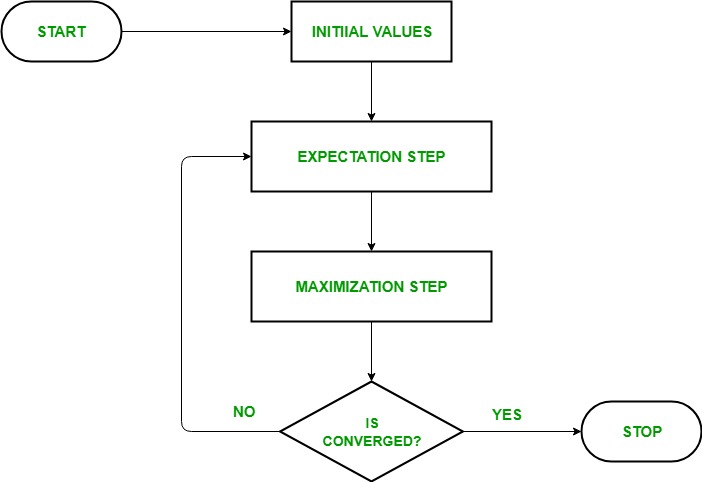
اینجا الگوریتمی است که باید دنبال کنید:
با توجه به مجموعه ای از داده های ناقص، با مجموعه ای از پارامترهای اولیه شروع کنید.
مرحله انتظار (E – step): در این مرحله انتظار، با استفاده از دادههای مشاهده شده موجود از مجموعه داده، میتوان مقادیر دادههای از دست رفته را تخمین زد یا حدس زد. در نهایت، پس از این مرحله، داده های کاملی را بدون مقادیر گمشده دریافت می کنیم.
مرحله حداکثر سازی (M – step): حال باید از داده های کاملی که در مرحله انتظار تهیه شده است استفاده کرده و پارامترها را به روز کنیم.
مرحله 2 و مرحله 3 را تکرار کنید تا به راه حل خود همگرا شویم.
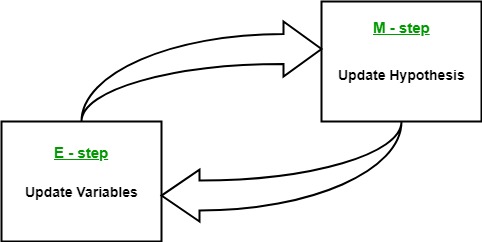
هدف از الگوریتم انتظار-بیشینه سازی
هدف الگوریتم Expectation-Maximization استفاده از داده های مشاهده شده موجود از مجموعه داده برای تخمین داده های از دست رفته متغیرهای پنهان و سپس استفاده از آن داده ها برای به روز رسانی مقادیر پارامترها در مرحله حداکثر سازی است.
اجازه دهید الگوریتم EM را به روشی دقیق درک کنیم:
مرحله راهاندازی: در این مرحله، مقادیر پارامترها را با مجموعهای از مقادیر اولیه مقداردهی اولیه کردیم، سپس مجموعه دادههای مشاهدهشده ناقص را با این فرض که دادههای مشاهدهشده از یک مدل خاص یعنی توزیع احتمال میآیند، به سیستم میدهیم.
مرحله انتظار: در این مرحله با استفاده از داده های مشاهده شده مقادیر داده های گم شده یا ناقص را تخمین یا حدس می زنیم. برای به روز رسانی متغیرها استفاده می شود.
مرحله حداکثر سازی: در این مرحله از داده های کامل تولید شده در مرحله “انتظار” برای به روز رسانی مقادیر پارامترها یعنی به روز رسانی فرضیه استفاده می کنیم.
مرحله بررسی همگرایی: اکنون در این مرحله بررسی کردیم که آیا مقادیر همگرا هستند یا خیر، اگر بله، متوقف شوید در غیر این صورت این دو مرحله یعنی مرحله “انتظار” و مرحله “بیشینه سازی” را تا زمانی که همگرایی رخ دهد تکرار کنید.
مزایا و معایب الگوریتم EM
👉 مزایا
دو مرحله اساسی الگوریتم EM یعنی E-step و M-step اغلب برای بسیاری از مشکلات یادگیری ماشین از نظر پیاده سازی بسیار آسان است.
راه حل برای M-stepsاغلب به شکل بسته وجود دارد.
همیشه تضمین شده است که مقدار درستنمایی پس از هر تکرار افزایش می یابد.
👈 معایب
همگرایی کندی دارد.
فقط به بهینه محلی همگرا می شود.
احتمالات رو به جلو و عقب را در نظر می گیرد. این چیز برخلاف بهینه سازی عددی است که فقط احتمالات رو به جلو را در نظر می گیرد.
کاربردهای الگوریتم EM
مدل متغیر پنهان چندین کاربرد واقعی در یادگیری ماشین دارد:
👉 برای محاسبه چگالی گاوسی یک تابع استفاده می شود.
👉 پر کردن داده های از دست رفته در طول نمونه مفید است.
👉 در حوزه های مختلف مانند پردازش زبان طبیعی (NLP)، بینایی کامپیوتر و غیره کاربرد فراوانی پیدا می کند.
👉 مورد استفاده در بازسازی تصویر در زمینه پزشکی و مهندسی سازه.
👉 برای تخمین پارامترهای مدل پنهان مارکوف (HMM) و همچنین برای برخی از مدل های ترکیبی دیگر مانند مدل های مخلوط گاوسی و غیره استفاده می شود.
👉 برای یافتن مقادیر متغیرهای پنهان استفاده می شود.
مورد استفاده از الگوریتم EM
مبانی توزیع گاوسی
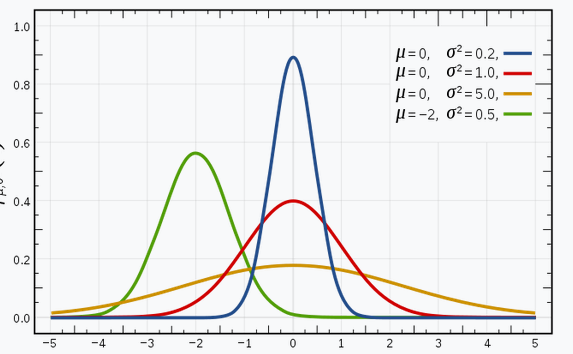
من مطمئن هستم که شما با توزیع های گاوسی (یا توزیع نرمال) آشنا هستید زیرا این توزیع به شدت در زمینه یادگیری ماشین و آمار استفاده می شود. منحنی زنگولهای دارد که مشاهدات به طور متقارن حول میانگین (متوسط) توزیع شدهاند.
تصویر نشان داده شده دارای چند توزیع گاوسی با مقادیر مختلف میانگین (μ) و واریانس (σ2) است. به یاد داشته باشید که هرچه مقدار σ (انحراف استاندارد) بیشتر باشد، میزان گسترش در امتداد محور بیشتر خواهد بود
در فضای 1 بعدی، تابع چگالی احتمال یک توزیع گاوسی به صورت زیراست:
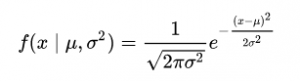
که در آن μ نشان دهنده میانگین و σ2 نشان دهنده واریانس است.
اما این فقط برای یک متغیر در 1-D صادق است. در مورد دو متغیر، به جای یک منحنی زنگوله دوبعدی مانند شکل زیر، یک منحنی زنگوله سه بعدی خواهیم داشت:
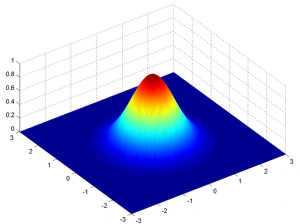
تابع چگالی احتمال به صورت زیر است:
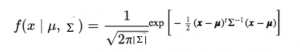
که در آن x بردار ورودی، μ بردار میانگین 2 بعدی، و Σ ماتریس کوواریانس 2×2 است. می توانیم همین را برای بعد d تعمیم دهیم.
بنابراین، برای مدل گاوسی چند متغیره، x و μ را به عنوان بردارهایی با طول d داریم، و Σ یک ماتریس کوواریانس d x d خواهد بود.
بنابراین، برای مجموعه دادهای که دارای d ویژگی است، مخلوطی از k توزیع گاوسی خواهیم داشت (که k نشاندهنده تعداد خوشهها است)، که هر یک دارای یک بردار میانگین و ماتریس واریانس هستند.
اما سوال ما این است: “چگونه می توانیم میانگین و واریانس هر گاوسی را دریابیم؟”
برای یافتن این مقادیر از تکنیکی به نام حداکثرسازی انتظار (EM) استفاده می کنیم.
مدل های مخلوط گاوسی
فرض اصلی این مدل های مخلوط این است که تعداد معینی از توزیع های گاوسی وجود دارد و هر یک از این توزیع ها نشان دهنده یک خوشه است. از این رو، یک مدل مخلوط گاوسی سعی می کند مشاهدات متعلق به یک توزیع واحد را با هم گروه بندی کند.
مدلهای مخلوط گاوسی مدلهای احتمالی هستند که از رویکرد خوشهبندی نرم برای توزیع مشاهدات در خوشههای مختلف یعنی توزیع گاوسی متفاوت استفاده میکنند.
به عنوان مثال، مدل مخلوط گاوسی از 2 توزیع گاوسی
ما دو توزیع گاوسی داریم – N(𝜇1، 𝜎12) و N(𝜇2، 𝜎22)
در اینجا باید در مجموع 5 پارامتر را تخمین بزنیم:
𝜃 = ( p، 𝜇1، 𝜎12، 𝜇2، 𝜎22)
که در آن p احتمال این است که داده ها از توزیع گاوسی اول و 1-p از توزیع گاوسی دوم می آیند.
سپس، تابع چگالی احتمال (PDF) مدل مخلوط با استفاده از:
g(x|𝜃) = p g1(x| 𝜇1، 𝜎12) + (1-p)g2(x| 𝜇2، 𝜎22)
هدف: با یافتن 𝜃 = (p، 𝜇1، 𝜎12، 𝜇2، 𝜎22) از طریق تکرارهای EM به بهترین وجه برازش چگالی احتمال داده شده را به دست آوریم.

1 Comment
ممنون از سایت فوق العادتون