حداکثر سازی انتظارات (EM) یک الگوریتم کلاسیک است که در دهه 60 و 70 با کاربردهای متنوع توسعه یافته است. می‌توان از آن به‌عنوان یک الگوریتم خوشه‌بندی بدون نظارت استفاده کرد و برای کاربردهای NLP مانند تخصیص نهفته دیریکله¹، الگوریتم Baum-Welch برای مدل‌های پنهان مارکوف و تصویربرداری پزشکی گسترش داد. به عنوان یک روش بهینه سازی، جایگزینی برای گرادیان کاهشی و موارد مشابه با یک مزیت بزرگ که در بسیاری از شرایط، به روز رسانی ها را می توان به صورت تحلیلی محاسبه کرد. بیشتر از آن، این الگوریتم یک چارچوب انعطاف پذیر برای تفکر بهینه سازی است.

در این نوشته، ما با یک مثال خوشه بندی ساده شروع می کنیم و سپس الگوریتم را به طور کلی مورد بحث قرار می دهیم.

مثال : خوشه بندی بدون نظارت

موقعیتی را در نظر بگیرید که در آن نقاط داده متنوعی با ویژگی هایشان داریم. ما می خواهیم آنها را به گروه های مختلف اختصاص دهیم.

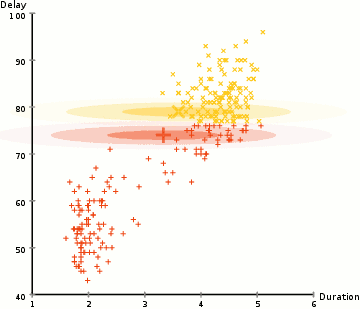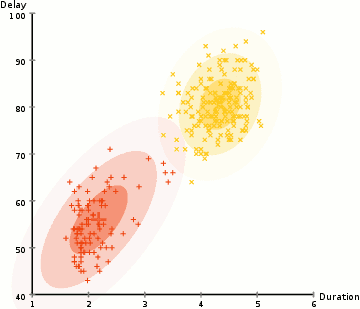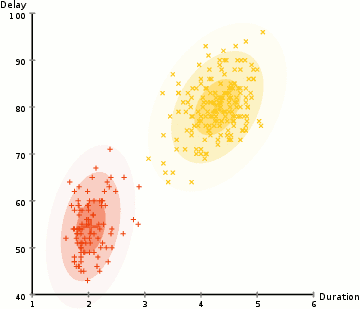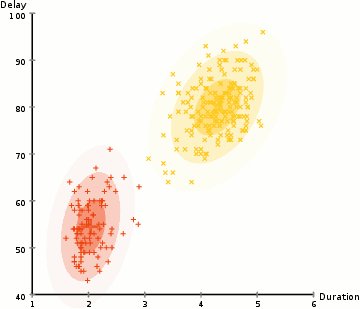
در مثال اینجا ما داده‌هایی درباره فوران‌های آبفشان نمادین Old Faithful در یلوستون داریم. برای هر فوران، طول آن و زمان از فوران قبلی را اندازه گیری کرده ایم. ما فرض می کنیم که دو “نوع” فوران وجود دارد (قرمز و زرد در نمودار)، و برای هر نوع فوران، داده های حاصل از یک توزیع نرمال (چند متغیری) تولید می شود. این مدل مخلوط گاوسی نامیده می شود.

مشابه خوشه‌بندی k-means، با یک حدس تصادفی برای اینکه آن دو توزیع/خوشه چیست شروع می‌کنیم و سپس با انجام دو مرحله متناوب، به طور تکراری بهبود می‌یابیم:

(انتظار) هر نقطه داده را به صورت احتمالی به یک خوشه اختصاص دهید. در این مورد، احتمال اینکه از خوشه قرمز و خوشه زرد آمده است را محاسبه می کنیم.

(بیشینه سازی) پارامترهای هر خوشه (میانگین وزن دار موقعیت و ماتریس واریانس-کوواریانس) را بر اساس نقاط موجود در خوشه (وزن دار شده با احتمال تخصیص آنها در مرحله اول) به روز کنید.
توجه داشته باشید که بر خلاف خوشه‌بندی k-means، مدل ما مولد است: هدف آن این است که فرآیند تولید داده‌ها را به ما بگوید. و به نوبه خود می‌توانیم مدل را دوباره نمونه‌برداری کنیم تا داده‌های (جعلی) بیشتری تولید کنیم.

حال می خواهیم یک مثال 1 بعدی با معادلات انجام دهیم.

نقاط داده را با یک ویژگی x در نظر بگیرید. ما فرض می کنیم که اینها توسط 2 خوشه تولید می شوند که هر کدام دارای توزیع نرمال N(μ, σ²) هستند. احتمال تولید داده توسط اولین خوشه π است.

بنابراین ما 5 پارامتر داریم: یک احتمال اختلاط π، و یک میانگین μ و انحراف استاندارد σ برای هر خوشه. من آنها را در مجموع به عنوان θ نشان خواهم داد.

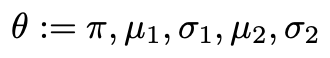
احتمال مشاهده نقطه داده با مقدار x چقدر است؟ اجازه دهید تابع احتمال-چگالی توزیع نرمال با ϕ نشان داده شود. برای اینکه نشانه گذاری کمتر به هم ریخته شود، به جای واریانس معمول از انحراف استاندارد به عنوان پارامتر استفاده می کنم.

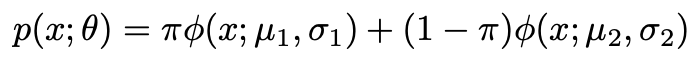
احتمال (درستنمایی) مشاهده کل مجموعه داده ما از n نقطه :

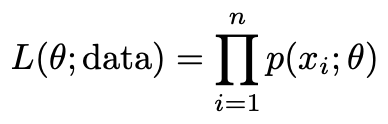
و ما معمولاً لگاریتم این تابع را میگیریم تا معادلات خود را به یک مجموع قابل کنترل‌تر تبدیل کنیم، یعنی لگاریتم درستنمایی:

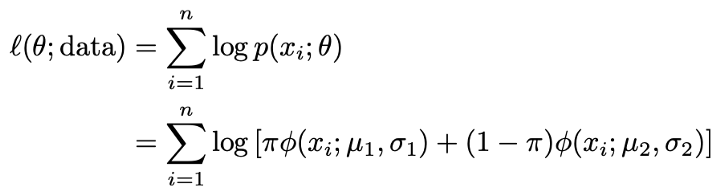
هدف ما این است که این عبارت را به حداکثر برسانیم: ما می‌خواهیم پارامترهایمان آنهایی باشند که داده هایی که مشاهده کردیم محتمل ترین باشد (یک برآوردگر بیشینه درستنمایی).

حال سوال این است که چگونه آن را بهینه کنیم؟ انجام این کار به طور مستقیم و تحلیلی به دلیل مجموع در لگاریتم دشوار خواهد بود.

ترفند این است که تصور کنیم یک متغیر پنهان وجود دارد که ما آن را Δ می نامیم. این یک متغیر باینری (0/1-ارزش) است که تعیین می‌کند یک نقطه در خوشه 1 باشد یا خوشه 2. اگر ما Δ را برای هر نقطه بدانیم، محاسبه تخمین‌های بیشینه درستنمایی پارامترهایمان بسیار آسان خواهد بود. برای راحتی انتخاب ما از 1 بودن Δ برای خوشه دوم، π را تغییر می دهیم تا احتمال وجود یک نقطه در خوشه دوم باشد.

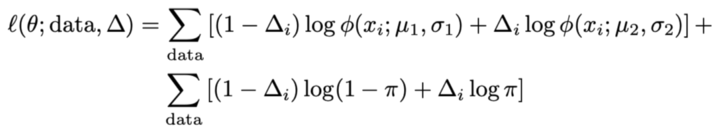
توجه داشته باشید که در حال حاضر مجموع ها خارج از لگاریتم هستند. همچنین، برای محاسبه درستنمایی مشاهده هر Δ، جمع اضافی را انتخاب می کنیم.

با فرض خلاف واقع که ما Δ را مشاهده کردیم، تخمین حداکثر درستنمایی آسان است. برای μ، میانگین نمونه را در هر خوشه بگیرید. برای σ، به همین ترتیب انحراف معیار (فرمول جمعیت، که MLE است). برای π، نسبت نمونه نقاط در خوشه دوم. اینها برآوردگرهای بیشینه درستنمایی معمول برای هر پارامتر هستند.

البته ما Δ نمی دانیم. راه حل این مورد قلب الگوریتم انتظار-بیشینه سازی است. طرح ما این است:

1. با انتخاب اولیه دلخواه پارامترها شروع کنیم.
   2. (انتظار) تخمینی از Δ.
   3. (بیشینه سازی) برآوردگرهای بیشینه درستنمایی را برای به روز رسانی تخمین پارامترمان محاسبه می کنیم.
   مراحل 2 و 3 را برای همگرایی تکرار کنید.
   باز هم، ممکن است فکر کردن به خوشه‌بندی k-means، جایی که ما همان کار را انجام می‌دهیم، مفید باشد. در خوشه بندی k-means، هر نقطه را به نزدیکترین مرکز (مرحله انتظار) نسبت می دهیم. در اصل، این یک تخمین سخت از Δ است. سخت است زیرا برای یکی از خوشه ها 1 و برای بقیه 0 است. سپس مرکزها را به‌روزرسانی می‌کنیم تا میانگین نقاط خوشه باشند (مرحله حداکثرسازی). این برآوردگر بیشینه درستنمایی برای μ است. در خوشه‌بندی k-means، «مدل» برای داده‌ها انحراف معیار ندارد.

در مثال، ما به جای آن یک تخصیص نرم از Δ را انجام می دهیم. ما گاهی اوقات به این مسئولیت می گوییم (مسئولیت هر خوشه برای هر مشاهده چقدر است). ما مسئولیت را به عنوان ɣ نشان خواهیم داد.

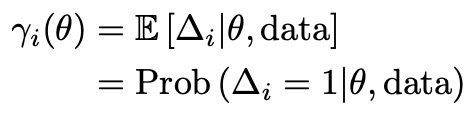
اکنون می توانیم الگوریتم کامل این مثال را یادداشت کنیم. اما قبل از انجام این کار، به سرعت جدولی از نمادهایی را که تعریف کرده‌ایم مرور می‌کنیم (تعداد زیادی وجود دارد).

و این هم الگوریتم:

توجه داشته باشید که تخمین های μ و σ برای خوشه 1 مشابه هستند اما در عوض از 1–ɣ به عنوان وزن استفاده می کنند.

اکنون که نمونه‌ای از الگوریتم را آورده‌ایم، امیدواریم احساسی نسبت به آن داشته باشید. ما در نوشته های بعدی به طور کلی به بحث در مورد الگوریتم خواهیم پرداخت.