بازنمایی تنک در پردازش تصویر
اکتبر 10, 2020sift flow algorithm | الگوریتم جریان سیفت
اکتبر 16, 2020SIFT Flow: ارتباطات متراکم بین صحنه ها و کاربردهای آن
چکیده- در حالی که هم ترازی تصویر در حوزه های مختلف بینایی کامپیوتری برای دهه ها مورد مطالعه قرار گرفته است، تراز کردن تصاویری که صحنه های مختلف را به تصویر می کشند یک مشکل چالش برانگیز باقی مانده است. مشابه جریان نوری که در آن یک تصویر با قاب مجاور زمانی خود تراز می شود، ما SIFT flow را پیشنهاد می کنیم،که روشی برای تراز کردن یک تصویر با نزدیک ترین همسایگان خود در یک پیکره بزرگ تصویر حاوی صحنه های مختلف است. الگوریتم جریان SIFT شامل تطبیق ویژگی های SIFT با نمونه برداری متراکم و پیکسلی بین دو تصویر است در حالی که ناپیوستگی های مکانی را حفظ می کند.ویژگیهای SIFT امکان تطبیق قوی در نماهای مختلف صحنه/اشیاء را فراهم میکند، در حالی که مدل مکانی حفظ ناپیوستگی امکان تطبیق اشیاء واقع در بخشهای مختلف صحنه را فراهم میکند. آزمایشها نشان میدهند که رویکرد پیشنهادی جفتهای شامل صحنه پیچیده را که دارای تفاوتهای مکانی قابلتوجهی هستند، به خوبی تراز میکند.بر اساس جریان SIFT، ما یک چارچوب پایگاه داده بزرگ مبتنی بر تراز را برای تجزیه و تحلیل و سنتز تصویر پیشنهاد میکنیم، که در آن اطلاعات تصویر از نزدیکترین همسایهها به یک تصویر پرس و جو با توجه به تطابق صحنه متراکم منتقل میشود.این چارچوب در برنامههای کاربردی مشخص، مانند پیشبینی میدان حرکت از یک تصویر، سنتز حرکت از طریق انتقال شی، ثبت تصویر ماهوارهای و تشخیص چهره استفاده میشود.
INTRODUCTION
Image alignment, registration and correspondence are central topics in computer vision. There are several levels of scenarios in which image alignment dwells. The simplest level, aligning different views of the same scene, has been studied for the purpose of image stitching [51] and stereo matching [45], e.g. in Figure 1 (a). The considered transformations are relatively simple (e.g. parametric motion for image stitching and 1D disparity for stereo), and images to register are typically assumed to have the same pixel value after applying the geometric transformation.
The image alignment problem becomes more complicated for dynamic scenes in video sequences, e.g. optical flow estimation [12], [29], [38]. The correspondence between two adjacent frames in a video is often formulated as an estimation of a 2D flow field. The extra degree of freedom transitioning from 1D in stereo to 2D in optical flow introduces an additional level of complexity. Typical assumptions in optical flow algorithms include brightness constancy and piecewise smoothness of the pixel displacement field [3], [8]
Image alignment becomes even more difficult in the object recognition scenario, where the goal is to align different instances of the same object category, as illustrated in Figure 1 (b). Sophisticated object representations [4], [6], [19], [57] have been developed to cope with the variations of object shapes and appearances. However, these methods still typically require objects to be salient, similar, with limited background cluster
In this work, we are interested in a new, higher level of image alignment: aligning two images from different 3D scenes but sharing similar scene characteristics. Image alignment at the scene level is thus called scene alignment. As illustrated in Figure 1 (c), the two images to match may contain object instances captured from different viewpoints, placed at different spatial locations, or imaged at different scales. The two images may also contain different quantities of objects of the same category, and some objects present in one image might be missing in the other. Due to these issues the scene alignment problem is extremely challenging.
Ideally, in scene alignment we want to build correspondence at the semantic level, i.e. matching at the object class level, such as buildings, windows and sky. However, current object detection and recognition techniques are not robust enough to detect and recognize all objects in images. Therefore, we take a different approach for scene alignment by matching local, salient, and transform-invariant image structures. We hope that semantically meaningful correspondences can be established through matching these image structures. Moreover, we want to have a simple, effective, object-free model to align image pairs such as the ones in Figure 1 (c).
Inspired by optical flow methods, which are able to produce dense, pixel-to-pixel correspondences between two images, we propose SIFT flow, adopting the computational framework of optical flow, but by matching SIFT descriptors instead of raw pixels. In SIFT flow, a SIFT descriptor [37] is extracted at each pixel to characterize local image structures and encode contextual information. A discrete, discontinuity preserving, flow estimation algorithm is used to match the SIFT descriptors between two images. The use of SIFT features allows robust matching across different scene/object appearances and the discontinuity-preserving spatial model allows matching of objects located at different parts of the scene. Moreover, a coarse-to-fine matching scheme is designed to significantly accelerate the flow estimation process.
Optical flow is only applied between two adjacent frames in a video sequence in order to obtain meaningful correspondences; likewise, we need to define the neighborhood for SIFT flow. Motivated by the recent progress in large image database methods [28], [43], we define the neighbors of SIFT flow as the top matches retrieved from a large database. The chance that some of the nearest neighbors share the same scene characteristics with a query image increases as the database grows, and the correspondence obtained by SIFT flow can be semantically meaningful.
Using SIFT flow, we propose an alignment-based large database framework for image analysis and synthesis. The information to infer for a query image is transferred from the nearest neighbors in a large database to this query image according to the dense scene correspondence estimated by SIFT flow. Under this framework, we apply SIFT flow to two novel applications: motion prediction from a single static image, where a motion field is hallucinated from a large database of videos, and motion transfer, where a still image is animated using object motions transferred from a similar moving scene. We also apply SIFT flow back to the regime of traditional image alignment, such as satellite image registration and face recognition. Through these examples we demonstrate the potential of SIFT flow for broad applications in computer vision and computer graphics.
The rest of the paper is organized as follows: after reviewing the related work in Sect. 2, we introduce the concept of SIFT flow and the inference algorithm in Sect. 3. In Sect. 4, we show scene alignment examples using SIFT flow with evaluations.
In Sect. 5, we show how to infer the motion field from a single image, and how to animate a still image, both with the support of a large video database and scene alignment. We further apply SIFT flow to satellite image registration and face recognition in Sect. 6. After briefly discussing how SIFT flow fits in the literature of image alignment in Sect. 7, we conclude the paper in Sect. 8.
معرفی:
ترازبندی تصویر ، ثبت و ارتباطات موضوعات اصلی در بینایی رایانه است. چندین سطح از سناریو وجود دارد که در آن ترازبندی تصویر ساکن است. ساده ترین سطح ، هم تراز کردن نماهای مختلف از یک صحنه مشابه ، با هدف چسباندن تصویر [51] و تطبیق استریو [45] ، به عنوان مثال در شکل 1 (a) مورد مطالعه قرار گرفته است. تبدیلات در نظر گرفته شده نسبتاً ساده هستند (به عنوان مثال حرکت پارامتری برای اتصال تصویر و بی شباهتی برای استریو 1D) ، و تصاویربرای ثبت معمولی فرض می شوند که تصاویر برای ثبت پس از استفاده از تبدیل هندسی ، همان پیکسل برابر دارند.
مسئله تراز تصویر برای صحنه های پویا در توالی های ویدیویی پیچیده تر می شود ، به عنوان مثال برآورد جریان بصری در [12] ، [29] ، [38]. ارتباطات بین دو فریم مجاور در یک فیلم اغلب به عنوان تخمین یک میدان جریان 2D صورت می گیرد. درجه آزادی اضافی در حال انتقال از 1D در استریو به 2D در جریان نوری ، سطح اضافی پیچیدگی را ایجاد می کند. مفروضات معمول در الگوریتم های جریان نوری شامل ثابت بودن روشنایی و صافی قطعه ای در زمینه جابجایی پیکسل است [3] ، [8].
ترازبندی تصویر در سناریوی تشخیص شی ، جایی که هدف تراز نمونه های مختلف از همان دسته شی است ، همانطور که در شکل 1 (ب) نشان داده شده است ، حتی دشوارتر می شود. نمایش های شی پیچیده [4] ، [6] ، [19] ، [57] برای کنار آمدن با تغییرات شکل ها و شکل های ظاهری شی ساخته شده اند. با این حال ، این روشها هنوز هم معمولاً برجسته ، مشابه و با خوشه زمینه محدود را می طلبند
در این کار ، ما به یک سطح بالاتر از تراز تصویر علاقه مندیم: تراز کردن دو تصویر از صحنه های سه بعدی مختلف اما به اشتراک گذاری ویژگی های صحنه مشابه .به هم ترازی تصویر در سطح صحنه ، تراز بندی صحنه گفته می شود. همانطور که در شکل 1 (c) نشان داده شده است ، این دو تصویر برای تطبیق ممکن است حاوی نمونه هایی از شی باشد که از دیدگاه های مختلف گرفته شده اند ، در مکان های مختلف مکانی قرار گرفته اند یا در مقیاس های مختلف تصویر شده اند. این دو تصویر ممکن است حاوی مقادیر مختلفی از اشیا از یک دسته باشند و برخی از اشیا موجود در یک تصویر ممکن است در تصویر دیگر وجود نداشته باشد. با توجه به این مسائل ، مشکل تراز صحنه بسیار چالش برانگیز است.
در حالت ایده آل ، در تراز صحنه می خواهیم ارتباطات را در سطح معنایی ایجاد کنیم ، یعنی مطابقت در سطح کلاس شی ، مانند ساختمان ها ، پنجره ها و آسمان. با این حال ، تکنیک های تشخیص و شناسایی شی فعلی آنقدر قوی نیستند که بتوانند همه اشیا موجود در تصاویر را شناسایی و تشخیص دهند. بنابراین ، با تطبیق ساختارهای محلی ، برجسته و تغییر ناپذیر تصویر، روش دیگری برای ترازبندی صحنه در نظر می گیریم. ما امیدواریم که بتوان از طریق مطابقت با این ساختارهای تصویر ارتباطات معنادار ایجاد کرد. علاوه بر این ، ما می خواهیم یک مدل ساده ، موثر و بدون شی برای تراز کردن جفت های تصویر مانند نمونه های شکل 1 (c) داشته باشیم.
با الهام از روش های جریان نوری ، که قادر به ایجاد ارتباطات متراکم پیکسل به پیکسل بین دو تصویر هستند ، ما با استفاده از چارچوب محاسباتی جریان نوری ، جریان SIFT را پیشنهاد می دهیم ، اما با تطبیق توصیف گرهای SIFT به جای پیکسل های خام. در جریان SIFT ، یک توصیفگر SIFT [37] در هر پیکسل استخراج می شود تا ساختارهای محلی تصویر را مشخص کند و اطلاعات محتوایی را رمزگذاری کند. برای مطابقت توصیف گرهایSIFT بین دو تصویر ، از الگوریتم گسسته و ناپیوسته و برآورد جریان استفاده شده است. استفاده از ویژگی های SIFT امکان تطابق قوی در نمایش های مختلف صحنه / شی را فراهم می کند و مدل مکانی با حفظ ناپیوستگی اجازه می دهد تا اشیا واقع در قسمت های مختلف صحنه مطابقت داشته باشند. علاوه بر این ، یک طرح تطبیق درشت تا ریز برای تسریع قابل توجه روند تخمین جریان طراحی شده است.
جریان نوری فقط برای به دست آوردن ارتباطات معنی دار بین یک دو ویدئو مجاور در یک توالی ویدئویی اعمال می شود. به همین ترتیب ، ما باید همسایگی جریان SIFT را تعریف کنیم. با انگیزه پیشرفت اخیر در روشهای پایگاه داده تصویر بزرگ [28] ، [43] ، همسایگان جریان SIFT را به عنوان بهترین موارد بازیابی شده از یک پایگاه داده بزرگ تعریف می کنیم. این احتمال که برخی از نزدیکترین همسایگان از ویژگی های صحنه مشابه با یک تصویر پرس و جو برخوردار باشند ، با رشد پایگاه داده افزایش می یابد و ارتباطات به دست آمده توسط جریان SIFT می توانند معنی دار باشند.
با استفاده از جریان SIFT ، ما یک چارچوب پایگاه داده بزرگ مبتنی بر هم ترازی را برای تجزیه و تحلیل و سنتز تصویر پیشنهاد می کنیم. اطلاعات مربوط به استنباط یک تصویر پرس و جو از نزدیکترین همسایگان در یک پایگاه داده بزرگ با توجه به ارتباطات متراکم صحنه که توسط جریان SIFT تخمین زده شده است ، به این تصویر جستجوگر منتقل می شود. تحت این چارچوب ، ما جریان SIFT را به دو کاربرد جدید اعمال می کنیم: پیش بینی حرکت از یک تصویر ثابت ، که در آن یک میدان حرکت از یک پایگاه داده بزرگ از فیلم ها دچار اشتباه می شود و انتقال حرکت ، که در آن یک تصویر ثابت با استفاده از حرکت های جسم تبدیل یافته از یک صحنه متحرک مشابه ما همچنین جریان SIFT را به رژیم ترازبندی تصویر سنتی مانند ثبت تصاویر ماهواره ای و تشخیص چهره اعمال می کنیم. از طریق این مثال ها ما پتانسیل جریان SIFT برای کاربردهای گسترده در بینایی رایانه و گرافیک رایانه را نشان می دهیم.
بقیه مقاله به شرح زیر است: پس از بررسی کارهای مرتبط در بخش 2 ، ما مفهوم جریان SIFT و الگوریتم استنباط را در بخش 3 معرفی می کنیم.. دربخش 4 ، ما با استفاده از جریان SIFT با ارزیابی ، نمونه های هم ترازی صحنه را نشان می دهیم.در بخش. 5 ، ما نشان می دهیم که چگونه میدان حرکت را از یک تصویر واحد ، و چگونه می توان یک تصویر ثابت را متحرک کرد ، هم با پشتیبانی از یک پایگاه داده ویدیویی بزرگ و هم ترازی صحنه استنباط کنیم. ما همچنین جریان SIFT را برای ثبت تصاویر ماهواره ای و شناسایی چهره در بخش 6 اعمال می کنیم. پس از بحث کوتاه در مورد چگونگی قرار گرفتن جریان SIFT در ادبیات ترازبندی تصویر در بخش 7 ، مقاله را در بخش 8 به نتیجه می رسانیم.
3 THE SIFT FLOW ALGORITHM
3.1 Dense SIFT descriptors and visualization SIFT is a local descriptor to characterize local gradient information [37]. In [37], SIFT descriptor is a sparse feature representation that consists of both feature extraction and detection. In this paper, however, we only use the feature extraction component. For every pixel in an image, we divide its neighborhood (e.g. 16×16) into a 4×4 cell array, quantize the orientation into 8 bins in each cell, and obtain a 4×4×8=128- dimensional vector as the SIFT representation for a pixel. We call this per-pixel SIFT descriptor SIFT image.
To visualize SIFT images, we compute the top three principal components of SIFT descriptors from a set of images, and then map these principal components to the principa components of the RGB space, as shown in Figure 2. Via projection of a 128D SIFT descriptor to a 3D subspace, we are able to compute the SIFT image from an RGB image in Figure 2 (c) and visualize it in (d). In this visualization, the pixels that have similar color may imply that they share similar local image structures. Note that this projection is only for visualization; in SIFT flow, the entire 128 dimensions are used for matching.
Notice that even though this SIFT visualization may look blurry as shown in Figure 2 (d), SIFT images indeed have high spatial resolution as suggested by Figure 3. We designed an image with a horizontal step-edge (Figure 3 (a)), and show the 1st component of the SIFT image of (a) in (c). Because every row is the same in (a) and (c), we plot the middle row of (a) and (c) in (b) and (d), respectively. Clearly, the SIFT image contains a sharp edge with respect to the sharp edge in the original image
Now that we have per-pixel SIFT descriptors for two images, our next task is to build dense correspondence to match these descriptors.
3 الگوریتم جریان سیفت
3.1 توصیف متراکم SIFT و بصری سازی توصیفگر محلی SIFT برای توصیف اطلاعات شیب محلی است [37]. در [37] ، توصیفگر SIFT یک بازنمایی تنک ویژگی است که هم از استخراج و هم از تشخیص ویژگی تشکیل شده است. در این مقاله ، ما فقط از مولفه استخراج ویژگی استفاده می کنیم. برای هر پیکسل در یک تصویر ، همسایگی آن (به عنوان مثال 16 eg 16) را به یک آرایه سلول 4 × 4 تقسیم می کنیم ، جهت گیری را به 8 قسمت در هر سلول اندازه می گیریم و یک بردار بعدی 4 × 4 × 8 = 128- به عنوان بازنمایی SIFT برای یک پیکسل بدست می آید. ما به این توصیفگرSIFT هر پیکسل تصویر می گوییم.
برای تجسم تصاویر SIFT ، ما سه مولفه اصلی توصیفگرهای SIFT را از مجموعه ای از تصاویر محاسبه می کنیم ، و سپس این مولفه های اصلی را به مولفه های اصلی فضای RGB ترسیم می کنیم ، همانطور که در شکل 2 نشان داده شده است. با ترسیم توصیفگر 128 بعدی به یک فضای فرعی 3D ، ما قادر به محاسبه SIFT تصویر از یک تصویر RGB در شکل 2 (c) و تجسم آن در (d) هستیم. در این بصری سازی ، پیکسل هایی که رنگ مشابه دارند ممکن است به این معنی باشد که ساختارهای تصویر محلی مشابهی دارند. توجه داشته باشید که این طرح فقط برای تجسم است. در جریان SIFT ، از کل 128 بعد برای مطابقت استفاده می شود.
توجه داشته باشید که حتی اگر این تصویر SIFT تار به نظر برسد ، همانطور که در شکل 2 (d) نشان داده شده است ، تصاویر SIFT در واقع از وضوح مکانی بالایی برخوردار هستند ، همانطور که در شکل 3 پیشنهاد شده است. و اولین مولفه تصویر SIFT (a) را در (c) نشان دهید. از آنجا که هر سطر در (a) و (c) یکسان است ، ما به ترتیب سطر میانی (a) و (c) را در (b) و (d) رسم می کنیم. واضح است که ، تصویر SIFT حاوی یک لبه تیز با توجه به لبه تیز در تصویر اصلی است.
اکنون که توصیفگرهای SIFT به ازای هر پیکسل برای دو تصویر داریم ، وظیفه بعدی ما ایجاد ارتباطات متراکم برای مطابقت با این توصیف کنندگان است.
3.2 Matching Objective
We designed an objective function similar to that of optical flow to estimate SIFT flow from two SIFT images. Similar to optical flow [11], [12], we want SIFT descriptors to be matched along the flow vectors, and the flow field to be smooth, with discontinuities agreeing with object boundaries.Based on these two criteria, the objective function of SIFT flow is formulated as follows. Let p=(x, y) be the grid coordinate of images, and w(p)=(u(p), v(p)) be the flow vector at p. We only allow u(p) and v(p) to be integers and we assume that there are L possible states for u(p) and v(p), respectively.Let s1 and s2 be two SIFT images that we want to match. Set ε contains all the spatial neighborhoods (a four-neighbor system is used). The energy function for SIFT flow is defined as:
which contains a data term, small displacement term and smoothness term (a.k.a. spatial regularization). The data term in Eqn. 1 constrains the SIFT descriptors to be matched along with the flow vector w(p). The small displacement term in Eqn. 2 constrains the flow vectors to be as small as possible when no other information is available. The smoothness term in Eqn. 3 constrains the flow vectors of adjacent pixels to be similar. In this objective function, truncated L1 norms are used in both the data term and the smoothness term to account for matching outliers and flow discontinuities, with t and d as the threshold, respectively.
We use a dual-layer loopy belief propagation as the base algorithm to optimize the objective function. Different from the usual formulation of optical flow [11], [12], the smoothness term in Eqn. 3 is decoupled, which allows us to separate the horizontal flow u(p) from the vertical flow v(p) in message passing, as suggested by [47]. As a result, the complexity of the algorithm is reduced from O(L4) to O(L2) at one iteration of message passing. The factor graph of our model is shown in Figure 5. We set up a horizontal layer u and vertical layer v with exactly the same grid, with the data term connecting pixels at the same location. In message passing, we first update intra-layer messages in u and v separately, and then update inter-layer messages between u and v. Because the functional form of the objective function has truncated L1 norms, we use distance transform function [20] to further reduce the complexity, and sequential belief propagation (BP-S) [52] for better convergence.
3.2 هدف تطبیق
ما یک تابع هدف مشابه عملکرد نوری را برای تخمین جریان SIFT از دو تصویر SIFT طراحی کرده ایم. مشابه جریان نوری [11] ، [12] ، ما می خواهیم با عدم پیوستگی موافقت با مرزهای شی توصیف کننده های SIFT در طول بردارهای جریان مطابقت داشته باشند ، و میدان جریان صاف باشد . بر اساس این دو معیار ، تابع هدف جریان SIFT بصورت زیر فرموله می شود. بگذارید p = (x، y) مختصات شبکه تصاویر و w (p) = (u (p) ، v (p)) بردار جریان در p باشد. ما فقط اجازه می دهیم که u (p) و v (p) عدد صحیح باشند و فرض می کنیم که به ترتیب L حالت های ممکن برای u (p) و v (p) وجود دارد. بگذارید s1 و s2 دو تصویر SIFT باشند که می خواهیم مطابقت داشته باشند . مجموعه ε شامل تمام همسایگی های محلی است (از سیستم چهار همسایه استفاده می شود). تابع انرژی برای جریان SIFT به شرح زیر است:
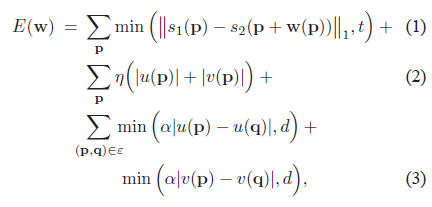
که شامل یک ترم داده ، ترم جابجایی کوچک و ترم صاف (نظم مکانی) است. اصطلاح داده در معادله 1 توصیگرهای SIFT است را مجبور می کند که با بردار جریان w (p) مطابقت داشته باشد. ترم کوچک جابجایی در معادله 2 بردارهای جریان را محدود می کند تا جایی که ممکن است اطلاعات دیگری در دسترس نباشد. ترم صافی در معادله 3 بردارهای جریان پیکسل های مجاور را به طور مشابه محدود می کند. در این تابع هدف ، نرم های کوتاه شده L1 در هر دو ترم داده و ترم صافی برای محاسبه فاصله های خارج و تداخل جریان ، به ترتیب با t و d به عنوان آستانه استفاده می شوند.
ما برای بهینه سازی تابع هدف از انتشار باورهای حلقه ای دو لایه استفاده می کنیم. ترم صافی در معادله 3 جداشده متفاوت از فرمول معمول جریان نوری [11] ، [12] ، است. که به ما امکان می دهد جریان افقی u (p) را جدا از جریان عمودی v (p) در پیام ارسال کنیم ، همانطور که توسط [47] پیشنهاد شده است. در نتیجه ، پیچیدگی الگوریتم در یک تکرار ارسال پیام از O (L4) به O (L2) کاهش می یابد. فاکتور گراف مدل ما در شکل 5 نشان داده شده است. ما یک لایه افقی u و لایه عمودی v با شبکه مشابه درست می کنیم ، با ترم داده پیکسل های متصل در همان مکان. در ارسال پیام ، ما ابتدا پیام های درون لایه را در u و v به طور جداگانه به روز می کنیم ، و سپس پیام های بین لایه ای بین u و v را به روز می کنیم. از آنجا که شکل عملکردی تابع هدف نرم های L1 کوتاه شده دارد ، از تابع تبدیل فاصله استفاده می کنیم [20] برای کاهش بیشتر پیچیدگی ، و انتشار باورهای متوالی (BP-S) [52] برای همگرایی بهتر.
3.3 Coarse-to-fine matching scheme
Despite the speed up, directly optimizing Eqn. (3) using this dual-layer belief propagation scales poorly with respect to image dimension. In SIFT flow, a pixel in one image can literally match to any pixels in the other image. Suppose the image has h2 pixels, then L ≈ h, and the time and space complexity of this dual-layer BP is O(h4). For example, the computation time for 145×105 images with an 80×80 search window is 50 seconds. It would require more than two hours to process a pair of 256×256 images with a memory usage of 16GB to store the data term.
To address the performance drawback, we designed a coarse-to-fine SIFT flow matching scheme that significantly improves the performance. The basic idea is to roughly estimate the flow at a coarse level of image grid, then gradually propagate and refine the flow from coarse to fine. The procedure is illustrated in Figure 6. For simplicity, we use s to represent both s1 and s2. A SIFT pyramid {s(k)} is established, where s(1) = s and s(k+1) is smoothed and downsampled from s(k). At each pyramid level k, let pk be the coordinate of the pixel to match, ck be the offset or centroid of the searching window, and w(pk) be the best match from BP. At the top pyramid level s(3), the searching window is centered at p3 (c3=p3) with size m×m, where m is the width (height) of s(3). The complexity of BP at this level is O(m4).After BP converges, the system propagates the optimized flow vector w(p3) to the next (finer) level to be c2 where the searching window of p2 is centered. The size of this searching window is fixed to be n×n with n=11. This procedure iterates from s(3) to s(1) until the flow vector w(p1) is estimated. The complexity of this coarse-to-fine algorithm is O(h2 log h), a significant speed up compared to O(h4). Moreover, we double η and retain α and d as the algorithm moves to a higher level of pyramid in the energy minimization.
When the matching is propagated from an coarser level to a finer level, the searching windows for two neighboring pixels may have different offsets (centroids). We modify the the distance transform function developed for truncated L1 norm [20] to cope with this situation, with the idea illustrated in Figure 7. To compute the message passing from pixel p to its neighbor q, we first gather all other messages and data term, and apply the routine in [20] to compute the message from p to q assuming that q and p have the same offset and range. The function is then extended to be outside the range by increasing α per step, as shown in Figure 7 (a). We take the function in the range that q is relative to p as the message.For example, if the offset of the searching window for p is 0, and the offset for q is 5, then the message from p to q is plotted in Figure 7 (c). If the offset of the searching window for q is −2 otherwise, the message is shown in Figure 7 (b).
Using the proposed coarse-to-fine matching scheme and modified distance transform function, the matching between two 256×256 images takes 31 seconds on a workstation with two quad-core 2.67 GHz Intel Xeon CPUs and 32 GB memory, in a C++ implementation. Further speedup (up to 50x) can be achieved through GPU implementation [16] of the BP-S algorithm since this algorithm can be parallelized. We leave this as future work.
A natural question is whether the coarse-to-fine matching scheme can achieve the same minimum energy as the ordinary matching scheme (using only one level).We randomly selected 200 pairs of images to estimate SIFT flow, and check the minimum energy obtained using coarse-to-fine scheme and ordinary scheme (non coarse-to-fine), respectively. For these 256 × 256 images, the average running time of coarse-tofine SIFT flow is 31 seconds, compared to 127 minutes in average for the ordinary matching. The coarse-to-fine scheme not only runs significantly faster, but also achieves lower energies most of the time compared to the ordinary matching algorithm as shown in Figure 8. This is consistent with what has been discovered in the optical flow community: coarse-tofine search not only speeds up computation but also leads to better solutions.
3.3 طرح تطبیق درشت و ریز
با وجود سرعت بالا ، به طور مستقیم بهینه سازی معادله 3 با استفاده از این انتشار باور دو لایه با توجه به بعد تصویر به طور ضعیف مقیاس بندی میکند. در جریان SIFT ، یک پیکسل در یک تصویر می تواند به معنای واقعی کلمه با هر پیکسل در تصویر دیگر مطابقت داشته باشد. فرض کنید تصویر دارای h2 پیکسل باشد ، سپس L ≈ h ، و پیچیدگی زمانی و مکانی این دو لایه BP (h4)o است. به عنوان مثال ، زمان محاسبه تصاویر 145 × 105 با پنجره جستجوی 80 × 80 50 ثانیه است. پردازش یک جفت عکس 256 × 256 با حافظه 16 گیگابایتی برای ذخیره ترم داده به بیش از دو ساعت زمان نیاز دارد.
برای رفع اشکال عملکرد ، ما یک طرح تطبیق جریان SIFT درشت تا ریز طراحی کردیم که عملکرد را به طور قابل توجهی بهبود می بخشد. ایده اصلی تخمین تقریبی جریان در سطح درشت شبکه تصویر ، سپس به تدریج انتشار و تصفیه جریان از درشت به ریز است. این روش در شکل 6 نشان داده شده است. برای سادگی ، از s برای نشان دادن s1 و s2 استفاده می کنیم. هرم SIFT {s (k)} ایجاد می شود ، جایی که s (1) = s و s (k + 1) صاف و از s (k) نمونه برداری می شود. در هر سطح هرم k ، بگذارید pk مختصات پیکسل برای مطابقت باشد ، ck انحراف یا مرکز پنجره جستجو باشد و w (pk) بهترین مطابقت از BP باشد. در سطح هرم بالایی s (3) ، پنجره جستجو در p3 (c3 = p3) با اندازه m × m قرار می گیرد ، جایی که m عرض (ارتفاع) s (3) است. پیچیدگی BP در این سطح O (m4) است.پس از همگرایی BP ، سیستم بردار جریان بهینه w (p3) را به سطح بعدی (ریزتر) منتقل می کند تا c2 باشد که در آن پنجره جستجوی p2 متمرکز است. اندازه این پنجره جستجو با n = 11 n × n ثابت شده است. این روش از s (3) تا s (1) تکرار می شود تا بردار جریان w (p1) تخمین زده شود. پیچیدگی این الگوریتم درشت تا ریز O (h2 log h) است ، سرعت قابل توجهی بالاتر از O (h4) است. علاوه بر این ، ما η را دو برابر می کنیم و α و d را حفظ می کنیم زیرا الگوریتم به سطح بالاتری از هرم در به حداقل رساندن انرژی می رسد.
هنگامی که تطبیق از یک سطح درشت به یک سطح دقیق تر منتشر می شود ، پنجره های جستجو برای دو پیکسل همسایه ممکن است انحراف های مختلفی (مراکز) داشته باشند. ما برای مقابله با این وضعیت ، تابع تبدیل فاصله ایجاد شده برای نرم L1 کوتاه [20] را اصلاح می کنیم ، با ایده ای که در شکل 7 نشان داده شده است. برای محاسبه پیام عبور از پیکسل p به همسایه q ، ابتدا همه پیام ها وترم داده های دیگر را جمع می کنیم ترم ، و روال را در [20] برای محاسبه پیام از p به q با فرض اینکه q و p جبران و دامنه یکسانی دارند ، اعمال کنید. همانطور که در شکل 7 (a) نشان داده شده است ، عملکرد با افزایش α در هر مرحله به خارج از محدوده گسترش می یابد. ما در محدوده ای که q نسبت به p است به عنوان پیام در نظر می گیریم.به عنوان مثال ، اگر جابجایی پنجره جستجو برای p صفر باشد و آفست q برابر 5 است ، پس پیام p از q در شکل 7 (c) رسم شده است. اگر در غیر این صورت انحراف پنجره جستجو برای q is2 باشد ، پیام در شکل 7 (ب) نشان داده شده است.
با استفاده از طرح تطبیق درشت و ریز پیشنهاد شده و عملکرد تبدیل فاصله اصلاح شده ، تطبیق بین دو تصویر 256 × 256 در یک ایستگاه کاری با دو پردازنده چهار هسته ای 2.67 گیگاهرتز Intel Xeon و 32 گیگابایت حافظه و در یک اجرای C ++ 31 ثانیه طول می کشد. سرعت بیشتر (تا 50 برابر) از طریق پیاده سازی GPU [16] الگوریتم BP-S حاصل می شود زیرا این الگوریتم می تواند موازی شود. ما این را به عنوان کار آینده می گذاریم.
یک سوال طبیعی این است که آیا طرح تطبیق درشت تا ریز می تواند به حداقل انرژی مشابه تطبیق معمولی برسد (فقط با استفاده از یک سطح). ما به طور تصادفی 200 جفت تصویر را برای تخمین جریان SIFT انتخاب کردیم و حداقل انرژی بدست آمده را با استفاده از طرح درشت از ریز و طرح عادی (غیر درشت از ریز) به ترتیب. برای این تصاویر 256 × 256 ، میانگین زمان جریان SIFT با ضخامت درشت 31 ثانیه است ، در حالی که برای مطابقت معمولی به طور متوسط 127 دقیقه است. طرح درشت تا ریز نه تنها به طور قابل توجهی سریعتر اجرا می شود ، بلکه در مقایسه با الگوریتم تطبیق معمولی که در شکل 8 نشان داده شده است ، انرژی کمتری را به دست می آورد. این با آنچه در جامعه جریان نوری کشف شده سازگار است: جستجوی tofine نه تنها سرعت محاسبات را افزایش می دهد بلکه به راه حل های بهتری نیز منجر می شود.
در این کار ، ما به یک سطح تراز بندی جدید و بالاتر از تراز تصویر علاقه مندیم: تراز کردن دو تصویر از صحنه های سه بعدی مختلف ، اما اشتراک ویژگی های صحنه مشابه. به هم ترازی تصویر در سطح صحنه ، تراز بندی صحنه گفته می شود. همانطور که در شکل 1 (c) نشان داده شده است ، این دو تصویر برای تطبیق ممکن است حاوی نمونه های جسمی باشد که از دیدگاه های مختلف گرفته شده اند ، در مکان های مختلف مکانی قرار گرفته اند یا در مقیاس های مختلف تصویر شده اند. این دو تصویر ممکن است حاوی مقادیر مختلفی از اشیا از یک دسته یکسان باشند و برخی از اشیا موجود در یک تصویر ممکن است در تصویر دیگر وجود نداشته باشد. با توجه به این مسائل ، مشکل تراز صحنه بسیار چالش برانگیز است.
